Pendulums and Almost Periodicity
Discussion
In the basement of Cardwell Hall, the Physics department has a display of two sets of pendulums linked by a spring. There is a movable bracket for each pair so you can start the two pendulums in a pair simultaneously in the same position or in opposite positions. One pair has two pendulums of the same length, and you can check that if you start them in symmetric (or anti-symmetric) positions, they will maintain their symmetry (or anti-symmetry). The other pair has two different length pendulums and in this case symmetry won't be maintained, instead you will have an apparently chaotic motion. In this assignment, you will work out the mathematics to describe these two situations.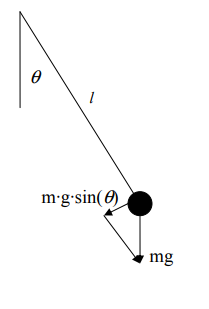 The traditional picture of a single pendulum is illustrated at the right. We ignore any friction, the
weight of the string or wire, and assume the only force acting on the mass at the end of the pendulum is
gravity. Since gravity pulls straight down, this force splits into two components, one of $mg\cos(\theta)$ which
acts in the direction of the pendulum (and produces tension in the wire or string which we will ignore)
and one of $mg\sin(\theta)$ which acts perpendicular to the pendulum (and makes the mass swing, which is what
we will study). Now by Newton's second law, force is mass times acceleration, where acceleration is the
second derivative of distance traveled with respect to time. Now the distance traveled by the mass as it
swings is given by $lq$, where $l$ is the length of the pendulum. So the differential equation to describe the
position of the pendulum is
$$
ml\frac{d^2\theta}{dt^2} = -mg \sin(\theta)
$$
where the negative sign indicates that when $\sin(\theta)$ is positive, the force is pushing to
decrease $\theta$ (and the reverse when $\sin(\theta)$ is negative). This is a non-linear equation.
If we assume the pendulum isn't swinging too
far, so the angle $\theta$ is small, then we can approximate this equation by a linear equation by
replacing $\sin(\theta)$ with its tangent line approximation near $\theta = 0$. Since $\sin(0) = 0$ and
$\sin'(0) = \cos(0) =1$, this means $\sin(\theta) \approx 0 + 1 \theta = \theta$ , so our equation becomes
$$
ml \frac{d^2\theta}{dt^2} = -mg\theta.
$$
1. From the linearized equation, justify Galileo's observation that the period of a pendulum depends only on
its length and not on the mass or the initial displacement.
The traditional picture of a single pendulum is illustrated at the right. We ignore any friction, the
weight of the string or wire, and assume the only force acting on the mass at the end of the pendulum is
gravity. Since gravity pulls straight down, this force splits into two components, one of $mg\cos(\theta)$ which
acts in the direction of the pendulum (and produces tension in the wire or string which we will ignore)
and one of $mg\sin(\theta)$ which acts perpendicular to the pendulum (and makes the mass swing, which is what
we will study). Now by Newton's second law, force is mass times acceleration, where acceleration is the
second derivative of distance traveled with respect to time. Now the distance traveled by the mass as it
swings is given by $lq$, where $l$ is the length of the pendulum. So the differential equation to describe the
position of the pendulum is
$$
ml\frac{d^2\theta}{dt^2} = -mg \sin(\theta)
$$
where the negative sign indicates that when $\sin(\theta)$ is positive, the force is pushing to
decrease $\theta$ (and the reverse when $\sin(\theta)$ is negative). This is a non-linear equation.
If we assume the pendulum isn't swinging too
far, so the angle $\theta$ is small, then we can approximate this equation by a linear equation by
replacing $\sin(\theta)$ with its tangent line approximation near $\theta = 0$. Since $\sin(0) = 0$ and
$\sin'(0) = \cos(0) =1$, this means $\sin(\theta) \approx 0 + 1 \theta = \theta$ , so our equation becomes
$$
ml \frac{d^2\theta}{dt^2} = -mg\theta.
$$
1. From the linearized equation, justify Galileo's observation that the period of a pendulum depends only on
its length and not on the mass or the initial displacement.
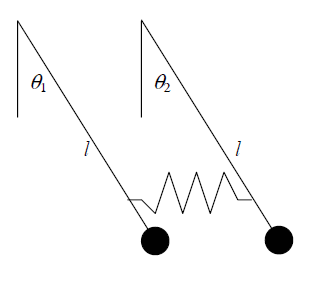 Next, we consider the case of two pendulums connected by a spring, as in the picture at the right.
First we assume the two pendulums have the same length and same mass, and the spring connecting them is
undamped with spring constant k. Then the linearized equations for this system are
$$ \begin{align}
ml\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k (l\theta_1 - l\theta_2) \\
ml\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k (l\theta_1 - l\theta_2)
\end{align} $$
where the difference in the sign of the term for the force of the spring between the two equations is because
the spring is pushing the two pendulums in opposite directions.
2. Show that in this system, if we have symmetric initial conditions, i.e. $\theta_1(0)=\theta_2(0)$, then the solutions are
symmetric, i.e. $\theta_1(t)=\theta_2(t)$ for all t.
3. Show that in this system, if we have antisymmetric initial conditions, i.e. $\theta_1(0)=-\theta_2(0)$, then the solutions are
antisymmetric, i.e. $\theta_1(t)=-\theta_2(t)$ for all t.
Problems 2 and 3 just ask you to verify the symmetry properties of the matched pendulums that were mentioned in the
opening paragraph and which you can observe if you try out the pendulums in the basement. You may find it useful to
note that if you want to show two functions are identical, it is sufficient to show their Laplace transforms are identical,
and if you want to show two functions are negatives of each other, it is sufficient to show their Laplace transforms
are negatives of each other.
Next, we consider the case of two pendulums connected by a spring, as in the picture at the right.
First we assume the two pendulums have the same length and same mass, and the spring connecting them is
undamped with spring constant k. Then the linearized equations for this system are
$$ \begin{align}
ml\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k (l\theta_1 - l\theta_2) \\
ml\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k (l\theta_1 - l\theta_2)
\end{align} $$
where the difference in the sign of the term for the force of the spring between the two equations is because
the spring is pushing the two pendulums in opposite directions.
2. Show that in this system, if we have symmetric initial conditions, i.e. $\theta_1(0)=\theta_2(0)$, then the solutions are
symmetric, i.e. $\theta_1(t)=\theta_2(t)$ for all t.
3. Show that in this system, if we have antisymmetric initial conditions, i.e. $\theta_1(0)=-\theta_2(0)$, then the solutions are
antisymmetric, i.e. $\theta_1(t)=-\theta_2(t)$ for all t.
Problems 2 and 3 just ask you to verify the symmetry properties of the matched pendulums that were mentioned in the
opening paragraph and which you can observe if you try out the pendulums in the basement. You may find it useful to
note that if you want to show two functions are identical, it is sufficient to show their Laplace transforms are identical,
and if you want to show two functions are negatives of each other, it is sufficient to show their Laplace transforms
are negatives of each other.
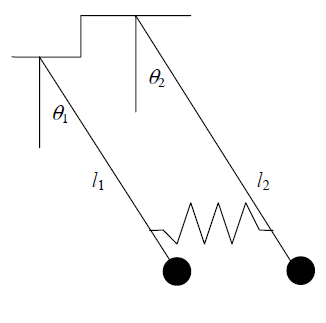 Finally, we come to the last case, where the pendulums have different lengths, as illustrated to the right.
In this case, we get nearly the same linearized system, except we need to put $l_1$ and $l_2$ in the appropriate locations.
$$ \begin{align}
ml_1\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k(l_1\theta_1 - l_2\theta_2) \\
ml_2\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k(l_1\theta_1 - l_2\theta_2) \\
\end{align} $$
Now we can solve this system and check that symmetry is no longer preserved. Rather than work with an arbitrary system,
we will pick particular values for the parameters.
4. Solve the system
$$ \begin{align}
ml_1\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k(l_1\theta_1 - l_2\theta_2) \\
ml_2\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k(l_1\theta_1 - l_2\theta_2) \\
\end{align} $$
where $m = 2 kg$, $l_1 = 1 m$, $l_2 = 1.1 m$, $g = 9.8 m/sec^2$, $k = 5 kg/sec^2$, and $\theta_1(0)=\theta_2(0)= \pi/36$ radians
(= $5\deg$).
In solving the system using Laplace transforms, you will encounter a biquadratic term in the denominator,
that is a term of the form $s^4 + ps^2 + q$. You can use the quadratic formula to factor this as
$(s^2 + a^2)(s^2 + b^2)$ and then use partial fractions to finish the problem. Of course, since these numbers aren't rigged,
the values you get for $p$, $q$, $a$, and $b$ are going to be messy and you will want to use decimal approximations
and then a calculator or computer to solve the system of equations you get from the partial fractions.
Note that the answer you get from this problem is of the form
$$ \begin{align}
\theta_1(t)&=A\cos(at)+B\cos(bt) \\
\theta_2(t)&=C\cos(at)+D\cos(bt)
\end{align} $$
As these functions are sums of periodic functions, they should be periodic with period $2\pi/r$, where $r$
is the least common multiple of $a$ and $b$, that is the smallest number which is an integer multiple of $a$ and $b$.
Unfortunately, the two curves you get for this particular problem aren't periodic (I just said they "should" be,
not that they actually are). The trick is that in this case our $a/b$ is an irrational number (which we have
approximated by a decimal), and so there is no common multiple $r$ which is an integer multiple of both $a$ and $b$.
So instead of having a simple pattern and then repeating it over and over each period, in this case the functions
never quite return to their original state and the system keeps shifting slightly each time. Functions of this form
are called "almost periodic." The study of almost periodic functions is a beautiful area of mathematics developed by
Harald Bohr, brother of the physicist Niels. Since there isn't a Nobel prize in mathematics, Harald never got a
Nobel prize like his brother. On the other hand, Niels didn't win an Olympic medal as a soccer star like Harald did.
Finally, we come to the last case, where the pendulums have different lengths, as illustrated to the right.
In this case, we get nearly the same linearized system, except we need to put $l_1$ and $l_2$ in the appropriate locations.
$$ \begin{align}
ml_1\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k(l_1\theta_1 - l_2\theta_2) \\
ml_2\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k(l_1\theta_1 - l_2\theta_2) \\
\end{align} $$
Now we can solve this system and check that symmetry is no longer preserved. Rather than work with an arbitrary system,
we will pick particular values for the parameters.
4. Solve the system
$$ \begin{align}
ml_1\frac{d^2\theta_1}{dt^2} &= -mg\theta_1 - k(l_1\theta_1 - l_2\theta_2) \\
ml_2\frac{d^2\theta_2}{dt^2} &= -mg\theta_2 + k(l_1\theta_1 - l_2\theta_2) \\
\end{align} $$
where $m = 2 kg$, $l_1 = 1 m$, $l_2 = 1.1 m$, $g = 9.8 m/sec^2$, $k = 5 kg/sec^2$, and $\theta_1(0)=\theta_2(0)= \pi/36$ radians
(= $5\deg$).
In solving the system using Laplace transforms, you will encounter a biquadratic term in the denominator,
that is a term of the form $s^4 + ps^2 + q$. You can use the quadratic formula to factor this as
$(s^2 + a^2)(s^2 + b^2)$ and then use partial fractions to finish the problem. Of course, since these numbers aren't rigged,
the values you get for $p$, $q$, $a$, and $b$ are going to be messy and you will want to use decimal approximations
and then a calculator or computer to solve the system of equations you get from the partial fractions.
Note that the answer you get from this problem is of the form
$$ \begin{align}
\theta_1(t)&=A\cos(at)+B\cos(bt) \\
\theta_2(t)&=C\cos(at)+D\cos(bt)
\end{align} $$
As these functions are sums of periodic functions, they should be periodic with period $2\pi/r$, where $r$
is the least common multiple of $a$ and $b$, that is the smallest number which is an integer multiple of $a$ and $b$.
Unfortunately, the two curves you get for this particular problem aren't periodic (I just said they "should" be,
not that they actually are). The trick is that in this case our $a/b$ is an irrational number (which we have
approximated by a decimal), and so there is no common multiple $r$ which is an integer multiple of both $a$ and $b$.
So instead of having a simple pattern and then repeating it over and over each period, in this case the functions
never quite return to their original state and the system keeps shifting slightly each time. Functions of this form
are called "almost periodic." The study of almost periodic functions is a beautiful area of mathematics developed by
Harald Bohr, brother of the physicist Niels. Since there isn't a Nobel prize in mathematics, Harald never got a
Nobel prize like his brother. On the other hand, Niels didn't win an Olympic medal as a soccer star like Harald did.
If you have any problems with this page, please contact bennett@ksu.edu.
©1994-2025 Andrew G. Bennett