Kansas State University

Discussion

The next question is how do we handle differential equations involving impulse functions? For example, consider a spring-mass system where the forcing function consists of an impulse (e.g. you hit it with a hammer). The most efficient way to handle this situation is with Laplace transforms (though it is possible to use variation of parameters). The key fact is that

Theorem: ${\mathcal L}\{\delta(t-c)\} = e^{-cs} $, provided $c\ge0$.

Proof: $$ \begin{align} {\mathcal L}\{\delta(t-c)\}&=\int_0^{\infty}\delta(t-c)e^{-st}\,dt \\ &=\int_{-c}^{\infty}\delta(u)e^{-s(u+c)}\,du \\ &=e^{-s(0+c)}=e^{-sc} \end{align} $$ With this in mind it is tempting to talk about an example like the following. But we will need to discuss some matters at the end before we are ready for a paradigm.

ALMOST CORRECT EXAMPLE: $$ \begin{align} x'' + x &= \delta(t) \\ x(0)&=0 \\ x'(0)&=0 \end{align} $$ We use exactly the same technique here as in the previous section.

Step 1: Take the Laplace transform of both sides of the equation. $$ \begin{align} {\mathcal L}\{x'' + x\} &= {\mathcal L}\{x''\} + {\mathcal L}\{x\} \\ &= s^2 {\mathcal L}\{x\} - sx(0) - x'(0) + {\mathcal L}\{x\} \\ &= (s^2 + 1){\mathcal L}\{x\} \\ {\mathcal L}\{\delta(t)\} &= e^{-0s}=1 \\ (s^2 + 1){\mathcal L}\{x\} &= 1 \end{align} $$ Step 2: Solve for ${\mathcal L}\{x\}$. $$ {\mathcal L}\{x\} = 1/(s^2 +1) $$ Step 3: Take the inverse Laplace transform to find the solution. $$ x(t) = \sin(t) $$ This looks good, but worried by the title, "Almost Correct Example," we now check our work. Observe that $x'(0)=1\ne0$ and so we have somehow failed to satisfy our initial values. What went wrong here? The difficulty lies in the nature of our initial values and our idealized impulse function. Consider a mass of $1kg$ on an undamped spring with spring constant $1kg/sec^2$. Initially at rest, the mass is subjected to an impulse at time 0 that instantaneously imparts an energy of 0.5 joules. The differential equation corresponding to this physical situation is exactly the differential equation of the example above, $x''+x=\delta(t)$. (You may try to work out for yourself why 0.5 joules corresponds to $\delta(t)$ instead of $0.5\delta(t)$. If you have questions stop by my office and I'll answer them.) The initial values are $x(0)=0$, $x'(0)=0$ since the system is initially at rest. But when the impulse hits, the energy of the impulse is instantaneously converted into kinetic energy which means that the velocity at time 0 instantaneously changes from 0 to 1. So our solution appears to have $x'(0)=1$, even though we found it using $x'(0)=0$. This is a physical justification for our answer. A mathematical justification is that our answer isn't actually $\sin(t)$. After all $\sin(-\pi/2)=-1$, but the mass is at rest prior to time 0 and so $x(-\pi/2)=0$ and not $-1$. Properly, we should write our answer as $$ x(t)=\left\{\eqalign{&0,\qquad t<0 \cr&\sin(t),\qquad t\ge0.\cr}\right. $$ Since this form is rather lengthy, we introduce one last function, the unit step function $$ u(t)=\left\{\eqalign{&0,\qquad t<0 \cr&1,\qquad t\ge0.\cr}\right. $$ Then we can write our answer to the previous example as $x(t)=u(t)\sin(t)$. The $u(t)$ reminds us that the mass is initially at rest and so $x(t)=0$ for all $t<0$. If we try to graph the solution $u(t)\sin(t)$ to the problem $x''+x=\delta(t)$, $x(0)=0$ and $x'(0)=0$ we get figure 1. The difficulty with our answer was that $x'(0)\ne0$ and if we look at figure 1, we see that this difficulty hasn't gone away. The graph has a corner at $t=0$ and so $x'$ doesn't exist at $t=0$. Mathematically, we reconcile our problems by defining the left and right derivatives. The left derivative at $t=0$ is the slope of the curve on the left side of $t=0$ and the right derivative at $t=0$ is the slope of the curve on the right side of $t=0$. In this case, the curve is horizontal to the left of $t=0$ and so the left derivative is 0. On the right side, the curve rises with a slope of 1 (remember that the horizontal and vertical scales are different) and so the right derivative is 1. We can then make our problem mathematically precise by saying that we want the solution to $x''+x=\delta(t)$ with initial values $x(0)=0$ and $x'(0)=0$ on the left.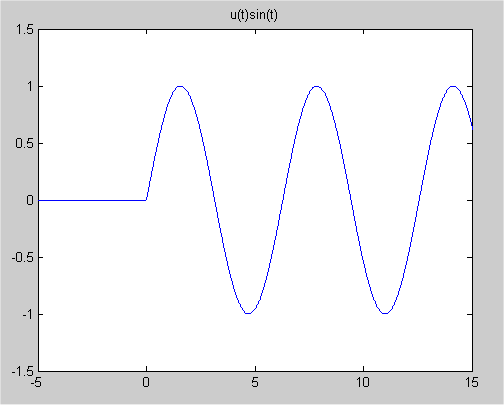

Paradigm

While we will usually pick our time scale so an impulse comes at $t=0$, this isn't always convenient. The usual way of writing an impulse at time $t=c$ is $\delta(t-c)$. Note that $t-c=0$ when $t=c$ so the delta function has its spike at $t=c$ in this case. We can handle such an impulse using the fact that ${\mathcal L}^{-1}\left\{e^{-cs}{\mathcal L}\{f\}\right\}=u(t-c)f(t-c)$, as noted in the table.

EXAMPLE: $$\begin{align} x''+5x'+6x&=\delta(t-1)\\ x(0)&=0\\ x'(0)&=0 \end{align}$$ Step 1: $$(s^2+5s+6){\mathcal L}\{x\}=e^{-s}$$ Step 2: $${\mathcal L}\{x\}=\frac{e^{-s}}{s^2+5s+6}$$ Step 3: Here we try to write ${\mathcal L}\{x\}$ in the form $e^{-cs}{\mathcal L}\{f\}$. We initially ignore the $e^{-s}$ term as we try to write the rest of our formula for ${\mathcal L}\{x\}$ as ${\mathcal L}\{f\}$ for some function $f$. $$\begin{align} \frac{1}{s^2+5s+6}&=\frac{1}{(s+2)(s+3)} \\ &=\frac{1}{s+2}-\frac{1}{s+3}\\ &={\mathcal L}\{e^{-2t}-e^{-3t}\} \end{align}$$ Now we can write $$ \frac{e^{-s}}{s^2+5s+6}=e^{-s}{\mathcal L}\{e^{-2t}-e^{-3t}\}$$ We choose $c=1$ since we have $e^{-s}$ and apply our rule that ${\mathcal L}^{-1}\{e^{-cs}{\mathcal L}\{f\}\}=u(t-c)f(t-c)$ to get $$\begin{align} x(t)&={\mathcal L}^{-1}\{\frac{e^{-s}}{s^2+5s+6}\}\\ &=u(t-1)(e^{-2(t-1)}-e^{-3(t-1)}) \end{align} $$ One case where we couldn't set our time scale to have the impulse occur at $t=0$ is when there is more than one impulse.

EXAMPLE: The following equation models a spring that receives an initial shock and then an aftershock half as strong 5 units of time later. $$\begin{align} x''+4x'+20x&=2\delta(t)+\delta(t-5)\\ x(0)&=0\\ x'(0)&=0 \end{align} $$ Step 1: Since the initial conditions are all 0, $$(s^2+4s+20){\mathcal L}\{x\}=2+e^{-5s}$$ Step 2: $${\mathcal L}\{x\}=\frac{2}{s^2+4s+20}+\frac{e^{-5s}}{s^2+4s+20}$$ Step 3: We initially ignore the numerators of both terms in ${\mathcal L}\{x\}$ and just concentrate on finding ${\mathcal L}^{-1}\{\frac{1}{s^2+4s+20}\}$. We compute $$\begin{align} \frac{1}{s^2+4s+20}&=\frac{1}{(s+2)^2+4^2}\\ &=\frac14\cdot\frac{4}{(s+2)^2+4^2} \end{align} $$ Now we use this to compute $$\begin{align} {\mathcal L}^{-1}\{\frac{2}{s^2+4s+20}\}&= 2{\mathcal L}^{-1}\{\frac{1}{s^2+4s+20}\} \\ &=2\frac{1}{4}u(t)e^{-2t}\sin(4t) \\ {\mathcal L}^{-1}\{\frac{e^{-5s}}{s^2+4s+20}\}&= {\mathcal L}^{-1}\{e^{-5s}{\mathcal L}\{\frac14e^{-2t}\sin(4t)\}\} \\ &=u(t-5)\frac14e^{-2(t-5)}\sin(4(t-5)) \end{align} $$ Finally, $x(t)$ is the sum of both of these, $$x(t)=\frac12u(t)e^{-2t}\sin(4t)+\frac14u(t-5)e^{-2(t-5)}\sin(4(t-5))$$ Note that the $u(t)$ and $u(t-5)$ terms here serve to indicate where each part of the solution is active. In particular, we need the $u(t-5)$ term to indicate that the part of the solution corresponding to the aftershock at $t=5$ doesn't affect the behavior of the system before the aftershock occurs!