Kansas State University

Discussion

First we will show that the Gamma function is an extension of the usual definition of factorial. The crucial feature of the factorial function is that $$ n!=n\times (n-1)! $$ and the Gamma function satisfies a similar relation.

Theorem $\Gamma(a+1)=a\Gamma(a)$

Proof $$ \begin{align} \Gamma(a+1)&=\int_0^{\infty}t^ae^{-t}\,dt \\ &=\left.-t^ae^{-t}\right|_0^{\infty}-\int_0^{\infty}-at^{a-1}e^{-t}\,dt \qquad\text{(integration by parts)} \\ &=a\int_0^{\infty}t^{a-1}e^{-t}\,dt \\ &=a\Gamma(a) \end{align} $$ So $\Gamma(a+1)$ satisfies the same relation as $a!$. In order to show that $\Gamma(a+1)=a!$ when $a$ is a positive integer it now suffices to show $\Gamma(1)=1$. A simple calculation shows that $$ \Gamma(1)=\Gamma(0+1)=\int_0^{\infty}e^{-t}\,dt=1 $$ So $\Gamma(2)=\Gamma(1+1)=1\Gamma(1)=1$ as well. And then $$ \begin{align} \Gamma(3)=2\Gamma(2)&=2\times1=2! \\ \Gamma(4)=3\Gamma(3)&=3\times2!=3! \\ \Gamma(5)=4\Gamma(4)&=4\times3!=4! \\ &\vdots \end{align} $$ So the Gamma function is an extension of the usual definition of factorial.

In addition to integer values, we can compute the Gamma function explicitly for half-integer values as well. The key is that $\Gamma(1/2)=\sqrt{\pi}$. Then $\Gamma(3/2)=1/2\Gamma(1/2)=\sqrt{\pi}/2$ and so on. The evaluation of the integral for $\Gamma(1/2)$ is done in problem 1 below. We can only write a closed form for the Gamma function at integers and half-integers. In other cases, like $\Gamma(1/3)$, we just have to write it in the integral form. We can approximate the integral numerically if we want to approximate something like $\Gamma(1/3)\approx2.67894$.

The key facts for the Gamma function as we've seen are that $\Gamma(a+1)=a\Gamma(a)$ and $\Gamma(1)=1$. We can use this relationship to extend the function to negative values as well. So while $\int_0^{\infty}t^ae^{-t}\,dt$ is undefined for $a\le-1$, we can define $\Gamma(-5/3)$ by using the rules.

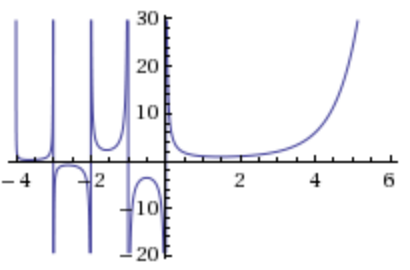
Image Generated by WolframAlpha

From the preceding analysis, you should realize that all we need to get a "reasonable" extension of the factorial function to non-integer values is to have a "nice" function which satisfies $f(a+1)=af(a)$ and $f(1)=1$. This is all we need to show $f(n+1)=n!$. We can build many such functions by taking any function $f$ we like defined for $1 \le a < 2 $ with $f(1)=1$ and extending it to other values of $a$ by using the relation $f(a+1)=af(a)$. So we can compute $f(5/2)=3/2f(3/2)$ and $f(3/2)$ is defined since $1\le 3/2 < 2$. As we shall see in the exercises though, you will want to make some requirements on the behavior of $f(a)$ near $a=2$ in order to make the function smooth, but there are lots of ways to do that. Now since there are many ways to extend the factorial function from the natural numbers to the real line, why is the Gamma function the right extension? Obviously one reason is it is what you get in computing the Laplace transform of $t^a$ for non-integer $a$. But the Gamma function is the correct extension in many other situations in mathematics. A (slightly technical) discussion of how mathematicians recognized that the Gamma function is the appropriate extension can be found in Leonhard Euler's Integral: An Historical Profile of the Gamma Function by Philip Davis. This article includes a graph of a "pseudogamma" function defined by letting $f(x)=1$ for $1< x \le 2$ and then extending to the whole line using the functional equations $f(x+1)=xf(x)$ as discussed above.

1. Justify steps (a) through (f) in the computation below showing $\Gamma(1/2)=\sqrt{\pi}$. $$ \begin{align} \Gamma(1/2)^2 &= \left(\int_0^{\infty}t^{-1/2}e^{-t}\,dt\right)^2 \\ &= \left(2\int_0^{\infty}e^{-x^2}\,dx\right)^2 \tag{a} \\ &= \left(\int_{-\infty}^{\infty}e^{-x^2}\,dx\right)^2 \tag{b} \\ &= \left(\int_{-\infty}^{\infty}e^{-x^2}\,dx\right)\left(\int_{-\infty}^{\infty}e^{-y^2}\,dy\right) \tag{c} \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-x^2}e^{-y^2}\,dxdy \tag{d} \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}\,dxdy \\ &= \int_{0}^{2\pi}\int_{0}^{\infty}e^{-r^2}\,rdrd\theta \tag{e} \\ &= \frac12\int_{0}^{2\pi}\int_{0}^{\infty}e^{-u}\,dud\theta \tag{f} \\ &= \frac12\int_{0}^{2\pi}\left.-e^{-u}\right|_0^{\infty}\,d\theta \\ &= \frac12\int_{0}^{2\pi}\,d\theta \\ &= \pi \end{align} $$

2. Evaluate
   1. $\Gamma(6)$
   2. $\Gamma(7/2)$
   3. $\Gamma(-5/2)$

3. We know $\Gamma(1)=1$. Why can't we use that to compute $\Gamma(0)$ using our basic rule that $\Gamma(n+1)=n\Gamma(n)$?

4. Why does $\displaystyle\lim_{t\downarrow 0}\Gamma(t)=\infty$?

5. Why must $\Gamma(t)$ have an asymptote for any negative integer $n$?

6. Show the following. You may assume $\Gamma(a)>0$ for $a>0$.
   1. $\Gamma(a)<0$ for $-1 < a < 0$.
   2. $\Gamma(a)>0$ for $-2 < a < -1$.

7. Show $g(x)=\Gamma(x)\Gamma(1-x)$ is a periodic function. In fact, $g(x)=\pi\csc(\pi x)$ but you don't need to show this (but after taking a course in complex variables you might want to try it).

In the remaining problems, suppose $f(a)$ is a function defined for $1\le a < 2$ and $F(a)$ is constructed as in the paragraph above with $F(a)=f(a)$ for $1\le a < 2$ and $F(a+1)=aF(a)$.
8. Show that if $f(a)=a$ for $1\le a<2$, then $F(a)$ is discontinuous.

9. Show that if $f(a)=1-a$ for $1\le a<2$, then $F(a)$ is discontinuous.

10. Show that if $f(a)=a^2-3a+3$ for $1\le a<2$, then $F(a)$ is continuous.

11. What is a necessary and sufficient condition on $f(a)$ for $F(a)$ to be continuous?

12. Show that if $f(a)=a^2-3a+3$ for $1\le a<2$, then $F(a)$ is not differentiable at $a=2$.

13. Show that if $f(a)=a^2/2-3a/2+2$ for $1\le a<2$, then $F(a)$ is differentiable at every $a$.

14. What is a necessary and sufficient condition on $f(a)$ for $F(a)$ to be differentiable?