Kansas State University

7. $\displaystyle \frac{1-\exp(-s)}{s(1+\exp(-s))} $

9. $\displaystyle \frac{(2-s)-(2+s)e^{-s}}{s^2(1-e^{-s})} $

11. $\displaystyle y(t)=\frac15e^{-t}+\frac{1}{10}\sin(2t)-\frac15\cos(2t).$

13. $y(t) = -(3/80)\cos(t) + (1/80)\sin(t) + (3/1040)\cos(3t) + (7/1040)\sin(3t) -(1/65)\exp(-2t) + (1/20)\exp(-t),$
or, if you use a calculator and get answers in decimal format (to the nearest 0.0001),
$y(t) = -0.0375\cos(t) + 0.0125\sin(t) + 0.0029\cos(3t) + 0.0067\sin(3t) -0.0154\exp(-2t) + 0.05\exp(-t).$

15. The Laplace transform of the solution is $$ \frac{1-\exp(-s)}{s(1+\exp(-s))(s^2+\pi^2)} $$ At $s=\pm i\pi$ both the $s^2+\pi^2$ term and the $1+\exp(-s)$ term are zero, so there is a double pole. Resonance is reasonable because the equation is undamped with natural (circular) frequency $\pi,$ hence the natural period is 2, and the square wave has period 2.

17. $$ \frac{e^x}{2}\int_0^x e^{-t^2-t}dt - \frac{e^{-x}}{2}\int_0^x e^{-t^2+t}dt $$ 19. The convolution integral is $$ \begin{align} \int_0^x \sin(x-u)\sec(u) du &= \int_0^x (\sin(x)\cos(u)-\cos(x)\sin(u))\sec(u) du \\ &= \sin(x)\int_0^x \cos(u)\sec(u) du - \cos(x)\int_0^x \sin(u)\sec(u) du \\ &= \sin(x)\int_0^x 1 du - \cos(x)\int_0^x \tan(u) du \\ &=x\sin(x)+\cos(x)\ln|\cos(x)| \end{align} $$ 21. $\displaystyle y(x) = \frac{e^x}{3} \int_0^x \frac{te^t}{(t-1)^2} dt -\frac{x}{3} \int_0^x \frac{e^{2t}}{(t-1)^2} dt.$
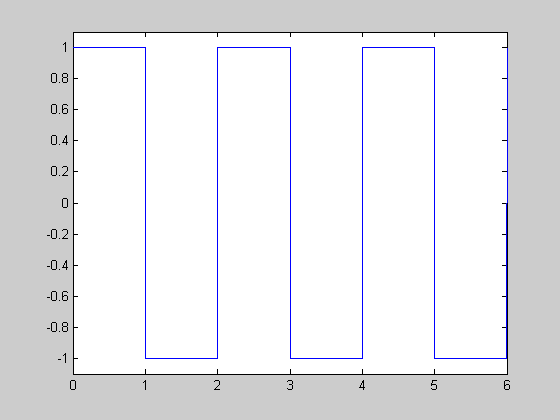
Laplace transforms aren't helpful here since the problem is not constant-coefficient, but variation of parameters still works.

23. $\displaystyle x(t) = e^{-t}+\frac12 u(t-2\pi)e^{2\pi-t}\sin(t) +\frac12 u(t-4\pi)e^{4\pi-t}\sin(t). $

25. $$ \begin{align} x(t) &= \exp(2t)(\cos(3t)+\frac13\sin(3t)) \\ y(t) &= \frac53\exp(2t)\sin(3t) \end{align} $$ 27. $$ \begin{align} x(t) &= \frac12\exp(3t)+\frac12\exp(3t) &= \frac12 \cosh(3t) \\ y(t) &= \frac32\exp(3t) + \frac32\exp(-3t) - \frac12\exp(2t) -\frac12\exp(-2t) &= \frac32\cosh(3t) - \frac12 \sinh(2t) \end{align} $$ 29.

• The solution curves spiral in to the equilibrium at $(-1,-1).$
• The equilibrium at $(1,1)$ is a saddle point.

31.

• The equilibrium at $(1,2)$ is a saddle point.
• The solution curves go directly out from the equilibrium at $(2,1).$
• The solution curves go directly in to the equilibrium at $(-2,-1).$
• The equilibrium at $(-1,-2)$ is a saddle point.

33.

• The solution curves go directly in to the equilibrium at $(1,1).$
• The equilibrium at $(0,0)$ is a saddle point.

35. $\displaystyle \exp(x+2y)=kx^3y^4$ or equivalently $\displaystyle y^4\exp(-2y)=\frac{K\exp(x)}{x^3}$ (where $K = 1/k$).

37. The equilibria are at $(0,0)$ and $\displaystyle \left(\frac{b}{n},\frac{a}{m}\right).$

39. $y^a\exp(-my)=kx^b\exp(-nx)$ where $k$ is an arbitrary constant.

41. The graphs in problem 40 show that as $t \to \infty$ either $(x(t),y(t)) \to (0,\infty)$ or $(x(t),y(t)) \to (\infty,0).$ So in either case one population tends to 0 which is in line with the exclusion principle.
(That the other population tends to $\infty$ rather than a finite value is unrealistic and is addressed in the next problem, but that isn't part of this problem).