Elementary Differential Equations

Math 340 Home, Textbook Contents, Online Homework Home

Numerical Methods For Higher Order Equations

Higher-Order Equations and First-Order Systems

In the last chapter we learned how to use the geometric interpretation of the solution of a first order equation as the integral curve following a slope field to compute numerical approximations to initial value problems, even when we couldn't find the exact solution. The situation is more complicated for higher order equations because now instead of just dealing with slope, $dy/dx$, the presence of terms like $d^2y/dx^2$ means a geometric analysis would include more involved concepts like curvature. Fortunately we can avoid this by transforming higher-order equations into first-order systems, and then sticking to the methods we already know.

Consider the equation $y''+3y'+2y=0$. We can convert this to a pair of first-order equations by introducing $v=dy/dx$. Then $dv/dx=d^2y/dx^2$ and the equation becomes $$ \begin{align} y'' + 3y' + 2y = 0& \\ \frac{dv}{dx} + 3v + 2y = 0& \\ \frac{dv}{dx} = -3v-2y& \end{align} $$ With this we see the second-order equation $y''+3y'+2y=0$ is the same as the first-order system $$ \begin{align} \frac{dy}{dx}&=v \\ \frac{dv}{dx} &= -3v-2y \end{align} $$ If you have initial values in the original equation, you just convert them to initial values for the system by making the same substitution. This technique of converting a second-order equation to a first-order system works for general equations, not just linear equations. If we have the initial value problem $\displaystyle\frac{d^2y}{dx^2}=f(x,y,y')$, $y(0)=y_0$, $y'(0)=y_1$, then this can be converted to the first-order system $$ \begin{align} \frac{dy}{dx}&=v,\qquad &y(0)=y_0 \\ \frac{dv}{dx}&=f(x,y,v),\qquad &v(0)=y_1 \end{align} $$ We can also convert higher-order equations to first order systems by making multiple substitutions. Consider the third-order equation $y'''+y''-2y'+xy=e^x$. Letting $v=dy/dx$ and $w=dv/dx=d^2y/dx^2$ we get $$ \begin{align} \frac{dy}{dx}&=v \\ \frac{dv}{dx}&=w \\ \frac{dw}{dx}&=e^x-xy+2v-w \end{align} $$ The technique of using Picard iteration to show that a "nice" first-order initial value problem has a solution applies to first order systems as well. You just have to make the integral in the Picard iteration vector-valued. You can see the proof of the following theorem in Math 540.

Theorem If $f(x,t_0,t_1,\ldots,t_n)$ and all its first partial derivatives are continuous in $(-h,h)\times(y_0-h,y_0+h)\times(y_1-h,y_1+h)\times\cdots\times(y_{n-1}-h,y_{n-1}+h)$ for some $h>0$, then there is an $\epsilon>0$ such that the initial value problem $$ \frac{d^ny}{dx^n}=f(x,y,y',\ldots,y^{(n-1)}),\qquad y(0)=y_0,\quad y'(0)=y_1,\quad\ldots\quad, y^{(n-1)}=y_{n-1} $$ has a unique solution for $x\in(-\epsilon,\epsilon)$ (note this statement asserts both the existence and uniqueness of the solution to the initial value problem).

Euler's Method

Just as for first-order equations, we often won't be able to find explicit solutions to higher-order equations and will want to find numerical approximations. We do this by converting the higher-order equations into first-order systems and then using the same techniques as we had in the last chapter. The difference is now we will apply these to all the different first-order equations in the system at once. We begin with Euler's method. As before, this method is well suited to implementation on a spreadsheet. We will use the example $$ y'' + 3y'+ 2y = 0,\qquad y(0)=1,\quad y'(0)=0. $$ Open Excel (or your favorite spreadsheet if you are working on your own computer). We'll start by labeling the columns to keep track of what goes where. Enter x into cell A1, dy/dx into cell B1, dv/dx into cell C1, y into cell D1, v=y' into cell E1, and h into cell H1. Next put the initial values and step-size into the appropriate starting spots with 0 in cell A2, 1 in cell D2, 0 in cell E2, and 0.1 in cell H2. Then put in the formulas with =A2+$H$2 in cell A3, =E2 in cell B3, =-3*E2-2*D2 in cell C3, =D2+$H$2*B3 in cell D3, and =E2+$H$2*C3 in cell E3. You now have the x column set to add the step size h as you move down each row, the dy/dx and dv/dx columns to compute the slopes based on the starting x, y, and v=y' values, and the y and v=y' columns to add h times dy/dx and h times dv/dx to the previous values for y and v respectively. Now click and drag to select cells A3..E3 and then click on the small square at the lower right of the box around those cells and drag it down for about 20 rows or so to copy the formulas down and automate the calculations.

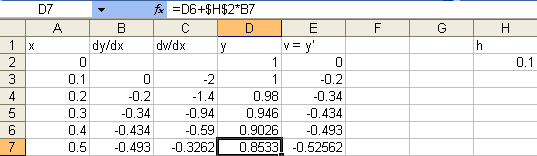
Note that the approximate values of the solution function $y(x)$ are contained in the y column which is column D, not the last column in the tableau. So here we see $y(0.5)\approx 0.8533$ for this initial value problem. Since this is a nice constant coefficient linear homogeneous equation, we can find the exact value is $y=2e^{-x}-e^{-2x}$ so we will be able to check our work. In cell F1 of the spreadsheet enter y exact and in cell G1 enter rel error (which stands for relative error). Then in cell F2 enter =2*exp(-A2)-exp(-2*A2) and in cell G2 enter =(F2-D2)/F2. It will be convenient to right-click on cell G2 and Format Cells as Percentage since relative error is a percent. Now click and drag to select cells F2 and G2 and drag those formulas down. This will show you how accurate the approximation produced by Euler's method is.

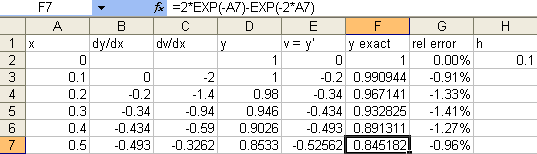
Euler's method isn't particularly accurate, though it works well enough in this problem with a relative error of about 1% (problems with exponential decay tend to work better than exponential growth). We can improve the approximation by taking smaller steps. If you change cell H2 to 0.05 to cut the step size in half, you find that the error in the value of $y(0.5)$ has been cut to about 0.43%. Of course you had to take 10 steps of size 0.05 to get to 0.5 while it only took 5 steps of size 0.1. So you do twice as much work but you cut the error roughly in half. This is the standard pattern for Euler's method, just as it was in for first-order equations.

Naturally, you can use this technique to handle other equations. The only thing you need to edit is the formula for dv/dx in column C. Do be sure to copy the edited formula down the whole column.

The Improved Euler Method

Just like for first-order equations, we can get more accuracy with the improved Euler's method. As before, you can use whatever tool you find most appropriate, but the simplest is probably the spreadsheet. We set things up similarly to the Euler's method, but with a couple of extra columns now for the extra computations. Enter x in cell A1, left dy/dx in cell B1, left dv/dx in cell C1, y tilde in cell D1, v tilde in cell E1, right dy/dx in cell F1, right dv/dx in cell G1, y in cell H1, v=y' in cell I1, and h in cell L1. Next enter the initial values 0 in cell A2, 1 in cell H2, 0 in cell I2, and 0.1 in cell L2. Then enter the formulas =A2+$L$2 in cell A3, =I2 in cell B3, =-3*I2-2*H2 in cell C3, =H2+$L$2*B3 in cell D3, =I2+$L$2*C3 in cell E3, =E3 in cell F3, =-3*E3-2*D3 in cell G3, =H2+$L$2*(B3+F3)/2 in cell H3, and =I2+$L$2*(C3+G3)/2 in cell I3. Now click and drag to select A3..I3 and then copy the formula down the sheet to repeat the calculations as far as you want.

As before we can set up columns for the exact values and the relative error to see how accurate this method is for this problem. Enter y exact in cell J1 and rel error in cell K1. Enter the formulas =2*exp(-A2)-exp(-2*A2) in cell J2 and =(J2-H2)/J2 in cell K2. As before it looks nicer if you set the format of the cells in column K to Percentage.

Note that the improved Euler's method is twice as much work as the original Euler's method, since you do an extra improvement step each row. On the other hand, the error for $y(0.5)$ is now just 0.21%, which is better than the -0.43% error we got by doing twice as much work with a smaller step size with the original Euler's method. We can improve the accuracy of our approximation further by using a smaller step size of $h=.05$. The result of this calculation is off by only 0.05% of the true value. While halving the step size (hence doubling the work) halved the error for Euler's method, it reduces the error in the improved Euler's method by about a factor of 4. Again, this is the same pattern as you saw for the first-order equations. And of course you can apply this method for other equations just by editing the formulas for the dv/dx in columns C and G.

Concluding Discussion

As noted above, to adjust to a different second-order equation you just need to change the column(s) for dv/dx. It is up to you to convert the second-order equation to a first order system and determine what the formula needs to be for $dv/dx$. It should be emphasized that the spreadsheets we've designed here are for second-order equations. If we had a third-order equation then, as discussed in the first section on this page, we would need a system of three equations. That would require columns for w and dw/dt in addition to those for y, v, dy/dt, and dv/dt. This isn't hard, but you do need to be sure you don't just blindly plug into the spreadsheets we've created if the problem doesn't fit.

We can extend the Runge-Kutta and Runge-Kutta-Feldman techniques to higher order equation by converting them to first-order systems in the same was as we have extended the Euler and Improved Euler method here. The same tradeoffs will apply. The RK and RKF methods are more accurate and preferred for careful computations. But for situations in which a fast runtime is more important that precise accuracy you may choose to use Euler's method or the improved Euler's method.

Exercises

Why do you only have to adjust the column(s) for dv/dx and not for dy/dx or anything else to change your spreadsheet to approximate a different equation?
Approximate $y(2)$ for the linear homogeneous initial value problem $$ \frac{d^2y}{dx^2}-\frac{dy}{dx}-6y=0,\qquad y(0)=1,\quad y'(0)=0 $$ using Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in Euler's method affect the relative error for this problem?
Approximate $y(2)$ for the linear homogeneous initial value problem $$ \frac{d^2y}{dx^2}+\frac{dy}{dx}-6y=0,\qquad y(0)=1,\quad y'(0)=0 $$ using the improved Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in the improved Euler's method affect the relative error for this problem?
Approximate $y(2)$ for the linear inhomogeneous initial value problem $$ \frac{d^2y}{dx^2}+4\frac{dy}{dx}+3y=e^x,\qquad y(0)=1,\quad y'(0)=0 $$ using Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in Euler's method affect the relative error for this problem?
Approximate $y(2)$ for the linear inhomogeneous initial value problem $$ \frac{d^2y}{dx^2}+4\frac{dy}{dx}+3y=e^x,\qquad y(0)=1,\quad y'(0)=0 $$ using the improved Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in the improved Euler's method affect the relative error for this problem?
Approximate $y(2)$ for the third-order linear initial value problem $$ \frac{d^3y}{dx^3}+2\frac{d^2y}{dx^2}-\frac{dy}{dx}-2y=0,\qquad y(0)=1,\quad y'(0)=0,\quad y''(0)=-1 $$ using Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in Euler's method affect the relative error for this problem?
Approximate $y(2)$ for the third-order linear initial value problem $$ \frac{d^3y}{dx^3}+2\frac{d^2y}{dx^2}-\frac{dy}{dx}-2y=0,\qquad y(0)=1,\quad y'(0)=0,\quad y''(0)=-1 $$ using the improved Euler's method with $h=0.1$ and $h=0.05$. How does cutting the step-size in half in the improved Euler's method affect the relative error for this problem?
Approximate $y(0.5)$ for the non-linear initial value problem $$ \frac{d^2y}{dx^2}-2y\frac{dy}{dx}=0,\qquad y(0)=1,\quad y'(0)=1 $$ using Euler's method with $h=0.1$ and $h=0.05$. The exact solution is $y(x)=\displaystyle\frac{1}{1-x}$ so $y(0.5)=2$. How does cutting the step-size in half in Euler's method affect the relative error for this non-linear problem.
Approximate $y(0.5)$ for the non-linear initial value problem $$ \frac{d^2y}{dx^2}-2y\frac{dy}{dx}=0,\qquad y(0)=1,\quad y'(0)=1 $$ using the improved Euler's method with $h=0.1$ and $h=0.05$. The exact solution is $y(x)=\displaystyle\frac{1}{1-x}$ so $y(0.5)=2$. How does cutting the step-size in half in the improved Euler's method affect the relative error for this non-linear problem.
(TRICKY) Approximate $y(1.1)$ for the non-linear initial value problem $$ \frac{d^2y}{dx^2}-2y\frac{dy}{dx}=0,\qquad y(0)=1,\quad y'(0)=1 $$ using the improved Euler's method with $h=0.1$. The exact solution is $y(x)=\displaystyle\frac{1}{1-x}$ so $y(1.1)=-10$. In this case the approximation is badly off. How small a step-size do you need to pick to get the relative error under 10%.