Elementary Differential Equations

Complex Numbers

Discussion

Now that we have learned a variety of techniques for handling first order equations, we will move on to higher order equations. Unfortunately, higher order equations can be a lot trickier. Fortunately, we will avoid most of the difficulties by only concentrating on the easy ones, which are also the most common in basic applications in engineering and physics (and when you get to the non-basic applications you should be ready to learn about the harder ones). The easy equations usually reduce down to solving polynomial equations, which is college algebra stuff. We won't be concerned with just the real roots of our polynomial equations though, we will have to consider the complex roots as well. And the complex roots we encounter will then have to be used in exponential functions. So before we begin solving the differential equations, we will take a couple of days to go over the theory of complex variables.

We let $i=\sqrt{-1}$. A complex number is a number of the form $a+bi$ where $a$ and $b$ are real numbers. Arithmetic with complex numbers is almost exactly the same as with real numbers except every time you square an $i$ you replace it with $-1$. There is also one new operation called conjugation where you replace $i$ by $-i$.

Complex Arithmetic

Real Part
$\Re(a + bi) = a$
$\Re(7 - 4i) = 7$

Imaginary Part
$\Im(a + bi) = b$
$\Im(3 - 11i) = -11$

Conjugation
$\overline{(a + bi)} = a - bi$
$\overline{(-2 + 5i)} = -2 - 5i$

Addition
$(a + bi) + (c + di) = (a + c) + (b + d)i$
$(2 + 3i) + (4 - 7i) = (2 + 4) + (3 - 7)i = 6 - 4i$

Subtraction
$(a + bi) - (c + di) = (a - c) + (b - d)i$
$(3 + 2i) - (-1 - 4i) = (3 - -1) + (2 - -4)i = 4 + 6i$

Multiplication
Here you just multiply out term by term and collect the like terms. $$\begin{align} (a + bi)(c + di) &= ac + adi + bci + bdi^2 \\ &= ac + adi + bci - bd \\ &= (ac - bd) + (ad + bc)i \\ (3 - 4i)(2 + i) &= (6 - -4) + (3 - 8)i = 10 - 5i \end{align} $$ Division:
This is the one tricky operation. The trick is to multiply the numerator and the denominator by the conjugate of the denominator. This will yield a real denominator and then everything is easy. $$ \eqalign {\frac{a+bi}{c+di}&=\frac{(a+bi)(\overline{c+di})}{(c+di)(\overline{c+di})} \cr &=\frac{(a+bi)(c-di)}{(c+di)(c-di)} \cr &=\frac{ac+bci-adi+bd}{c^2+cdi-cdi+d^2} \cr &=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}\cr &=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i \cr } $$ In the last step we use the fact that $c^2+d^2$ is a real number and we know that the quotient of a sum is the sum of the quotients and that we know how to divide by real numbers. The fact that when you multiply a complex number by its conjugate you get a real product is very important and will show up again. $$ \eqalign {\frac{2-7i}{3+i}&=\frac{(2-7i)(3-i)}{(3+i)(3-i)} \cr &=\frac{(6-7)+(-2-21)i}{(9+1)+(-3+3)i} \cr &=\frac{-1-23i}{10} \cr &=-0.1-2.3i \cr} $$

Complex Exponentials

Now that we can do arithmetic with complex numbers, we want to do calculus with them. We start with the exponential function. The trick is to expand the function in a Taylor series about the point $z=0$ and see what happens. In the following, $t$ denotes a real variable. You also need to use the following relations: $ i^2=-1$, $ i^3=-i$, $ i^4=1$, $ i^5=i$, etc. $$ \eqalign {e^{it}&=1+it+\frac{(it)^2}{2!}+\frac{(it)^3}{3!}+\frac{(it)^4}{4!} +\frac{(it)^5}{5!}+\cdots \cr &=1+it+\frac{i^2t^2}{2!}+\frac{i^3t^3}{3!}+\frac{i^4t^4}{4!} +\frac{i^5t^5}{5!}+\cdots \cr &=1+it-\frac{t^2}{2!}-i\frac{t^3}{3!}+\frac{t^4}{4!}+i\frac{t^5}{5!}-\cdots \cr &=\left(1-\frac{t^2}{2!}+\frac{t^4}{4!}-\cdots\right) +i\left(t-\frac{t^3}{3!}+\frac{t^5}{5!}-\cdots\right) \cr &=\cos(t)+i\sin(t) \cr} $$ as we recognize the Taylor series about 0 for cosine and sine. Using this relationship, we can now define the exponential of a general complex number as follows: $$ e^{x+iy}=e^xe^{iy}=e^x(\cos(y)+i\sin(y))$$ We will use this relation often in solving differential equations.

Geometry of Complex Numbers

Above we covered the basic arithmetic of complex numbers, which we will use to solve differential equations in later sections. Next we will give a geometric interpretation of complex numbers. This interpretation isn't necessary to solve differential equations, but most students find it helpful in understanding how complex numbers work.

Complex numbers don't lie on a number line but rather on the complex plane. Complex numbers can be written $x+iy$, where $x$ and $y$ are real. We naturally graph the number $x+iy$ at the point $(x,y)$. The $x$--axis is referred to as the Real axis and the $y$--axis as the Imaginary axis. We can also identify points in the plane using polar coordinates rather than rectangular coordinates. The polar coordinates of a complex number are called the modulus and the argument of the complex number, where modulus is the distance from the origin ($r$) and the argument is the angle made with the Real axis by the segment from the origin to the point ($\theta$). The modulus and argument of a complex number therefore have the same definitions as the usual conversion from rectangular to polar coordinates.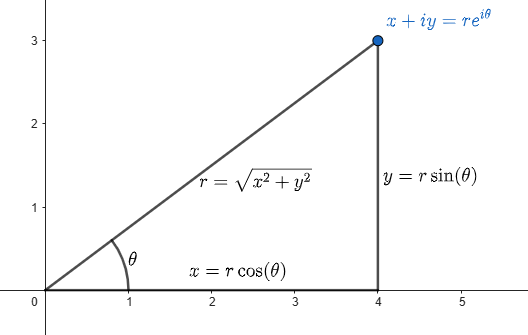

Modulus $$|x+iy|=\sqrt{x^2+y^2} $$ Argument $$ \arg(x+iy)=\left\{\eqalign{ &\arctan(y/x), \cr &\arctan(y/x)+\pi, \cr &\arctan(y/x)-\pi, \cr}\qquad \eqalign{x\ge0\cr x<0, y\ge0 \cr x<0, y<0 \cr } \right. $$ Recall that $\arctan$ is a $\pi$-periodic function, usually defined to take values from $-\pi/2$ to $\pi/2$. On the other hand, the argument of a complex number is a polar angle, which can range from $-\pi$ to $\pi$. That is why we have the somewhat complicated expression for the argument. If you are trying to compute an argument using a calculator, you can punch in $\arctan(y/x)$ but then you are responsible for deciding if you need to adjust by a factor of $\pm\pi$. On the other hand, many computer languages now include a atan2(x,y) function that computes the argument of the complex number $x+iy$ directly.

Once you have gone from rectangular to polar coordinates, the natural thing is to go from polar to rectangular coordinates. Suppose we have a complex number $z$ with modulus $|z|$ and argument $\arg(z)$. Then the real and imaginary parts of $z$ can be determined using the formulas for conversion from polar to rectangular coordinates.

Real Part: $\Re(z)=|z|\cos(\arg(z)) $

Imaginary Part: $\Im(z)=|z|\sin(\arg(z))$

We are now ready for a sneaky trick, that turns out to be very useful. If we write $z=\Re(z)+i\Im(z)$ and use the preceding rules for the real and imaginary parts and do a little bit of algebra and remember what we learned about complex exponentials in the previous section and don't worry about having the word ``and'' too many times in the same sentence we get $$ \eqalign { z&=\Re(z)+i\Im(z) \cr &=|z|\cos(\arg(z))+i|z|\sin(\arg(z)) \cr &=|z|\bigl(\cos(\arg(z))+i\sin(\arg(z))\bigl) \cr &=|z|\bigl(e^{0+i\arg(z)}\bigl) \cr &=|z|e^{i\arg(z)} \cr } $$ This formula is called the polar form of the complex number $z$. In the next section we will see how converting complex numbers from rectangular form $x+iy$ into polar form $re^{i\theta}$ and back again can simplify trig identities. For now we will concentrate on how understanding the polar form helps us understand the geometric meaning of the basic operations of complex arithmetic. Addition and subtraction of complex numbers are just vector addition and subtraction like you studied in Calculus III with this geometric interpretation of complex numbers as vectors in the plane. Multiplication and division are more complicated.

To understand the multiplication of complex numbers geometrically, it is easiest to work in polar coordinates. Suppose we want to multiply $re^{i\theta}$ and $se^{i\phi}$. We compute $$ \eqalign { re^{i\theta}\times se^{i\phi}&=rse^{i\theta}e^{i\phi} \cr &=rse^{i(\theta+\phi)} \cr } $$ So the modulus of the product is the product of the moduli and the argument of the product is the sum of the arguments. In other words, to multiply two complex numbers you multiply the lengths of the corresponding vectors (in polar coordinates) and add the angles (in polar coordinates). Division is just the reverse of course. You divide the moduli and subtract the angles.

Let us check how this interpretation works for $i^2$. The complex number $i$ is represented by the vector $(0,1)$ which has modulus 1 and argument $\pi/2$, that is to say it is a vector of length 1 and it is at a right angle with the Real axis. When we multiply this number by itself, we multiply the length by itself and $1\times1=1$ so the product will also have modulus 1. We add the argument to itself, and twice a right angle is a straight angle, so the vector should point in the negative real direction. And the vector of length 1 in the negative real direction represents the number $-1$, so we do indeed have $i^2=-1$.

Trig Identities Through Complex Exponentials

What does the graph of $3\cos(2x) + 4\sin(2x)$ look like? This is a difficult question for most people to answer without technology. While you know what the graphs of trig functions look like, adding them can get messy, involving plotting both graphs and then trying to add the heights. It turns out that using some trig identities you can rewrite $3\cos(2x) + 4\sin(2x)$ in the form $A\cos(\omega x-\phi)$ for the right choices of $A$, $\omega$ and $\phi$. This is just a cosine wave with amplitude $A$, circular frequency $\omega$, and phase shift $\phi$, so it is easier to visualize. But most students have difficulty remembering how the trig identities go, even when they are in trig, let alone several years later. Using complex polar coordinates, it is relatively easy to convert sums of cosine and sine functions to this nicer form.

The key to rewriting $3\cos(2x) + 4\sin(2x)$ using complex numbers is the following pair of facts: $\Re\left(3e^{2xi}\right)=3\cos(2x)$ and $\Re\left(-4ie^{2xi}\right)=4\sin(2x)$. So $$3\cos(2x)+4\sin(2x)=\Re\left(3e^{2xi}-4ie^{2xi}\right) =\Re\left((3-4i)e^{2xi}\right)$$ We now rewrite $3-4i$ in polar form (using the results from the previous section on complex variables). $$r=|3-4i|=\sqrt{3^2+4^2}=5\qquad\theta=\arctan(-4/3)\approx-.927$$ So $3 - 4i \approx 5e^{-.927i}$. Now we plug this into our representation for $3\cos(2x) + 4\sin(2x)$ and obtain $$ \begin{align} 3\cos(2x)+4\sin(2x)&=\Re\left((3-4i)e^{2xi}\right) \\ &\approx\Re\left(5e^{-.927i}e^{2xi}\right) \\ &=\Re\left(5e^{(2x-.927)i}\right) \\ &=5\cos(2x-.927) \end{align} $$

There will be some additional examples of places where thinking in terms of complex exponentials rather than trig functions is helpful in the exercises. We will also discover that complex exponentials can provide a more natural way to think about the solutions of linear constant coefficient differential equations.