Kansas State University

1. Using Euler's formula, $\exp(ix)=\cos(x)+i\sin(x),$ and the usual rules of exponents, establish De Moivre's formula, $$ \left(\cos(n\theta)+i\sin(n\theta)\right) = \left(\cos(\theta)+i\sin(\theta)\right)^n. $$
2. Use DeMoivre's formula to write the following in terms of $\sin(\theta)$ and $\cos(\theta)$.
   1. $\cos(6\theta)$
   2. $\sin(6\theta)$

---

One of the properties of the $\sin(x)$ and $\cos(x)$ that I hope you recall from trigonometry is that $\cos(x)$ is an even function, i.e. $\cos(-x)=\cos(x),$ while $\sin(x)$ is an odd function, i.e. $\sin(-x)=-\sin(x).$ We will see that any function can be split into pieces with these symmetries.

---

3. Given a general function $f(x),$ define $\displaystyle f_e(x)=\frac{f(x)+f(-x)}2$ and $\displaystyle f_o(x)=\frac{f(x)-f(-x)}2.$. Show
   1. $f(x)=f_e(x)+f_o(x),$ and

   2. $f_e(x)$ is an even function and $f_o(x)$ is an odd function.
   So every function can be split into even and odd pieces.

4. Given that $f(x)=f_e(x)+f_o(x)$ where $f_e(x)$ is an even function and $f_o(x)$ is an odd function, show that
   1. $\displaystyle f_e(x)=\frac{f(x)+f(-x)}2,$ and

   2. $\displaystyle f_o(x)=\frac{f(x)-f(-x)}2,$ and
   This shows the decomposition in the previous problem is the unique way to cut a function into even and odd pieces.

---

If we apply the decomposition developed in the previous two problems to the exponential function, we get the hyperbolic functions, $$ \begin{align} \cosh(x)&=\frac{\exp(x)+\exp(-x)}2 \\ \sinh(x)&=\frac{\exp(x)-\exp(-x)}2 \end{align} $$ These functions are covered in your calculus text, but sometimes that section is skipped. They are closely related to the usual trigonometric functions and you can define hyperbolic tangent, secant, cosecant, and cotangent in the obvious way (e.g. $\displaystyle \tanh(x)=\frac{\sinh(x)}{\cosh(x)}$). The next few problems give a quick overview of some of their properties.

---

5. Show
   1. $\cosh(ix)=\cos(x),$ and

   2. $\sinh(ix)=i\sin(x).$
   So the hyperbolic functions are just rotations of the usual trigonometric functions in the complex plane.

6. Verify the following hyperbolic trig identities.
   1. $\cosh^2(x)-\sinh^2(x)=1$

   2. $\cosh(s+t)=\cosh(s)\cosh(t)+\sinh(s)\sinh(t)$

   Note that these are almost the same as the corresponding identities for the regular trig functions, except for changes in the signs. You can derive hyperbolic identities corresponding to all the different identities you learned in trigonometry.

7. Invert the formula $\displaystyle \sinh(x)=\frac{\exp(x)-\exp(-x)}2$ to write $\sinh^{-1}(x)$ in terms of $\log(x).$ Note that you will need to use the quadratic formula to get the inverse.

8. Verify the following differentiation rules for the hyperbolic functions
   1. $\displaystyle \frac{d\sinh(x)}{dx}=\cosh(x),$ and

   2. $\displaystyle \frac{d\cosh(x)}{dx}=\sinh(x).$
   So for the hyperbolic functions you don't have to try to remember which derivative gets a minus sign.

9. Use the substitution $x=\sinh(u)$ to evaluate the integral $$ \int \frac{dx}{\sqrt{1+x^2}}. $$ This integral can also be evaluated with a trig substitution, but using a hyperbolic substitution simplifies the process.

10. Suppose $L$ is the operator defined by $Ly=Dy-3y$. Compute $L(\exp(x)).$

11. Suppose $L$ is the operator defined by $Ly=D^2y+3Dy+2y$. Compute $L(\exp(2x)).$

12. Suppose $L$ is the operator defined by $Ly=D^2y-3Dy+y$. Compute $L(\sin(x)).$

13. Suppose $L$ is the operator defined by $Ly=yDy$. Compute $L(2x^3).$

14. Show $Ly = Dy - xy$ is a linear operator. Remember you must show both parts of the definition hold for all functions $y$.

15. Show $Ly = D^2y + 3Dy - 4y$ is a linear operator. Remember you must show both parts of the definition hold for all functions $y$.

16. Show $Ly = Dy - xy^2$ is not a linear operator. Hint: It is sufficient to show $L(y + z) \ne Ly + Lz.$ for some choice of $y$ and $z$.

17. Show $Ly = yDy$ is not a linear operator. Hint: It is sufficient to show $L(y + z) \ne Ly + Lz.$ for some choice of $y$ and $z$.

18. Suppose $L$ is a linear operator and we have three partial particular solutions,
    • $y_{p1}$ with $Ly_{p1}=f_1$
    • $y_{p2}$ with $Ly_{p2}=f_2$
    • $y_{p3}$ with $Ly_{p3}=f_3$
    Show $y=ay_{p1}+by_{p2}+cy_{p3}$ is a particular solution to $Ly=af_1+bf_2+cf_3$.

19. Show $\exp(x)$ and $\exp(2x)$ are linearly independent.

20. Show $\exp(rx)$ and $\exp(sx)$ are linearly independent if $r\ne s$.

21. Show $\exp(rx)$ and $x\exp(rx)$ are linearly independent for every $r.$

---

The equation for a freely hanging chain (or wire or what-have-you) is $$ \frac{d^2y}{dx^2}=\frac{\delta g}{H}\sqrt{1+\left(\frac{dy}{dx}\right)^2} $$ where $y$ and $x$ are the vertical and horizontal coordinates of the chain, $\delta$ is the linear density of the chain, $g$ is the acceleration of gravity, and $H$ is the horizontal tension in the chain. The curve that solves this equation is called a catenary, after the Latin word for "chain." If you are curious about the derivation of this equation, you are welcome to come by my office and ask about it. This is a second-order non-linear equation. In general, we won't tackle such problems in this course, but this one has the special feature that $y$ never appears by itself. You only see its derivatives, $\displaystyle \frac{dy}{dx}$ and $\displaystyle \frac{d^2y}{dx^2}.$ That allows us to use a special trick to reduce this to a first-order equation, which we can actually solve.

(Image from Wikimedia user Kamel15 under a Creative Commons License)

---

22. Suppose $\delta g/H=2$ so the equation for the catenary becomes $$ \frac{d^2y}{dx^2}=2\sqrt{1+\left(\frac{dy}{dx}\right)^2}. $$ Make the substitution $\displaystyle p=\frac{dy}{dx}.$ This leads to a separable equation is $p$ and $x.$ Solve this equation for $p(x)$ (the integral in problem 9 will be helpful). Then back-substitute and integrate $\displaystyle \frac{dy}{dx}=p(x)$ to find the solution. Note that you will get one arbitrary constant from the separable equation and a second arbitrary constant from the integration in the back-substitution, giving you the two arbitrary constants you expect for a second-order equation.

23. Match the equations on the right with the factorings on the left.

    $(D+x)(D+2)y=0$ $(D+2)(D+x)y=0$ $(D+x)(D+x)y=0$

    $y''+(x+2)y'+(2x+1)y=0$ $y''+(x+2)y'+2xy=0$ $y''+2xy'+(x^2+1)y=0$

24. Match the equations on the right with the factorings on the left.

    $(D+x)(D-x)y=0$ $(D-x)(D+x)y=0$ $(D+x^2)(D-1)y=0$

    $y''+(x^2-1)y'-x^2y=0$ $y''-(x^2+1)y=0$ $y''-(x^2-1)y=0$

25. Expand the following equations into the form $y''+p(x)y'+q(x)y=0.$
    1. $(D+x)(D-1)y=0$
    2. $(D-1)(D+x)y=0$

26. Expand the following equations into the form $y''+p(x)y'+q(x)y=0.$
    1. $(D+2x)(D+3)y=0$
    2. $(D+3)(D+2x)y=0$

27. Expand the following equations into the form $y''+p(x)y'+q(x)y=0.$
    1. $(D+a(x))(D+b(x))y=0$
    2. $(D+b(x))(D+a(x))y=0$

28. Based on the results of previous problem, when will $$(D+a(x))(D+b(x))y=(D+b(x))(D+a(x))y,$$ i.e. when do the operators commute?

---

Once you have factored a second order linear differential operator as $Lu = RSu$, you can solve $Lu=f$ by first solving $Rv=f$ and then $Su=v$. Using this, find the general solutions to the following problems.

---

29. Find the general solution to $(D+2x)(D+1)y=0.$

30. Find the general solution to $(D+1)(D+2x)y=0.$

31. Find the general solution to $(D+1)(D+2x)y=\exp(x).$

32. Solve $(D-r)y=0$, justifying the claim made in point 1 of the text section on homogeneous equations.

33. Solve $(D-r)^2y=0$, justifying the claim made in point 2 of the text section on homogeneous equations.

34. Assume the solution of $(D-r)^ny=0$ is $y=C_{n-1}x^{n-1}e^{rx} + C_{n-2}x^{n-2}e^{rx} + \cdots + C_0e^{rx}.$ Using this assumption, show that the solution of $(D-r)^{n+1}y=0$ is $y=C_{n}'x^{n}e^{rx} + C_{n-1}'x^{n-1}e^{rx} + \cdots + C_0'e^{rx}$ (where we use C_0' so we don't get confused about the two sets of arbitrary constants).

---

We can use the result in the previous problem to justify the claim made in point 3 of the text section on homogeneous equations. Problems 1 and 2 have shown the result is true for $n=0$ and $n=1.$ Then by problem 3 since the result is true for $n=1,$ it is also true for $n=1+1=2.$ But then since the result is true for $n=2,$ it must also be true for $n=3.$ And continuing, it must be true for all $n.$ This general process of proving something is true for a starting value, and then proving if it is true for one value, it will also be true for the next value, and concluding the statement is then always true is called mathematical induction.

---

35. Write the form for the particular solution to $$ y''+4y'+3y=e^{2x}+x^2+1 $$ You just need the form with the undetermined coefficents, you don't need to actually find the particular solution.

36. Write the form for the particular solution to $$ y''+4y'+3y=xe^{-x}-\cos(3x) $$ You just need the form with the undetermined coefficents, you don't need to actually find the particular solution.

37. Write the form for the particular solution to $$ y''+4y=\sin(2x)-x^2e^x $$ You just need the form with the undetermined coefficents, you don't need to actually find the particular solution.

38. Write the form for the particular solution to $$ y''+6y'+25y=x\exp(-3x)\cos(4x) $$ You just need the form with the undetermined coefficents, you don't need to actually find the particular solution.

39. Find the general complex solution to the differential equation $$\frac{d^2y}{dz^2}-2\frac{dy}{dz}+10y=0.$$
40. Find the general complex solution to the differential equation $$\frac{d^2y}{dz^2}+4\frac{dy}{dz}+8y=0.$$
41. Find the general complex solution to the differential equation $$\frac{d^2y}{dz^2}+4y=z.$$
42. Find the general complex solution to the differential equation $$\frac{d^2y}{dz^2}+y=\exp(iz).$$
43. Solve the complex initial value problem $$ \begin{align} \frac{d^2y}{dz^2}+3\frac{dy}{dz}+2y&=0 \\ y(0)&=2+i \\ y'(0)&=3 \end{align} $$
44. Find the complex general solution to the differential equation $$ \frac{d^2y}{dz^2}+25y=0. $$
45. Using the complex general solution you found in problem 44, solve the initial value problem $$ \begin{align} \frac{d^2y}{dz^2}+25y&=0, \\ y(0)&=2, \\ y'(0)&=0 \end{align} $$ Show that the answer you get is a real function, illustrating that a linear differential equation with real coefficients and real initial data will have a real solution.

46. Consider the differential operator $$Ly=\frac{d^2y}{dx^2}-2y\frac{dy}{dx}.$$
    1. Show two homogeneous solutions of $Ly=0$ are $y_1=\tan(x)$ and $y_2=-\tanh(x).$
    2. In general, $y=c_1y_1(x)+c_2y_2(x)$ is not a solution to the equation $Ly=0$ for this operator. Why can't we just take linear combinations here like we did in the text section on homogeneous equations?

47. When solving a polynomial equation in algebra, once you find one solution you can factor it out to get an equation of smaller degree. We can do something similar with linear differential equations. Suppose $v(x)$ is a solution to the second-order linear equation, $y''+p(x)y'+q(x)y=0.$ Substitute $y=v(x)w(x)$ in the equation and show you get a differential equation involving $w'$ and $w'',$ but not $w$ by itself. This new equation can be reduced to a first-order equation using the trick from problem 22 (but you just have to get the equation, not reduce the degree).

48. For first-order equations we discovered that solution curves never cross. This was because if two solutions crossed, then we would have two different solutions to the corresponding initial value problem and that's not allowed by the existence and uniqueness theorem. We have a corresponding existence and uniqueness theorem for higher-order equations (which is given in the section on numerical methods for higher-order equations). However, solution curves for a higher-order equation may cross. Why doesn't this violate the existence and uniqueness theorem?
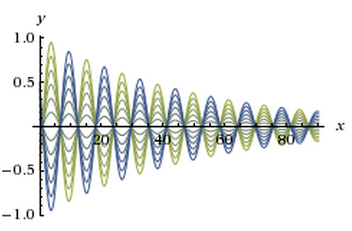
    Solution curves for $y'' + 0.04y' + 0.3y = 0$.
    (Graph produced by WolframAlpha)

    ---

    As derived in the text, underdamped free motion has the form $$ \begin{align} x(t)&=A\exp\left(-\frac{ct}{2m}\right)\cos(\omega_1t+\phi) \\ \omega_1&=\sqrt{\frac{k}{m}-\left(\frac{c}{2m}\right)^2}. \end{align} $$ This motion is quasi-periodic. That means the motion isn't periodic (since the amplitude is decaying) but the time between successive upcrossings (or downcrossings or maxima or minima) is constant (and, naturally, this time is called the quasi-period). It is straightforward to compute the spring constant of a spring. But computing the damping coefficient is difficult to do directly. A standard way to do so is to use the quasi-period. You'll work out the details of this below.

    ---

49. Suppose a spring-mass system has a mass of $200g,$ a spring constant of $100g/sec^2,$ and a damping constant of $10g/sec.$ What is the (circular) quasi-frequency, $\omega_1,$ of the damped motion?

50. Suppose a spring-mass system has a mass of $70kg,$ a spring constant of $7kg/sec^2,$ and a damping constant of $28kg/sec.$ What is the (circular) quasi-frequency, $\omega_1,$ of the damped motion?

 
51. Suppose a spring-mass system has a mass of $200g,$ a spring constant of $100g/sec^2,$ and a damping constant of $10g/sec.$ What is the quasi-period of the damped motion?

52. Suppose a spring-mass system has a mass of $70kg,$ a spring constant of $7kg/sec^2,$ and a damping constant of $28kg/sec.$ What is the quasi-period of the damped motion?

53. Suppose a spring-mass system has a mass of $100g,$ a spring constant of $10g/sec^2,$ and a damping constant of $20g/sec.$ What is the quasi-period of the damped motion?

54. Suppose a spring-mass system has a mass of $250g,$ a spring constant of $150g/sec^2,$ and a damping constant of $1000g/sec.$ What goes wrong and why when you try to compute the quasi-period?

 
55. A spring-mass system has mass $500g$ and spring constant $150g/sec^2.$ The quasi-period is measured at 14.8 seconds. What is the damping constant of the spring-mass system (to the nearest $0.1 g/sec$)?

56. A spring-mass system has mass $140g$ and spring constant $700g/sec^2.$ The quasi-period is measured at 2.9 seconds. What is the damping constant of the spring-mass system (to the nearest $0.1 g/sec$)?

 
57. If $m$ has units of $g,$ $k$ has units of $g/sec^2$ (or equivalently $ergs/cm$), and $c$ has units of $g/sec$ (or equivalently $ergs/(cm/sec)$),
    1. What are the units of (circular) quasi-frequency, $\omega_1,$ and
    2. What are the units of quasi-period?

58. Show that increasing the damping of a spring-mass system increases the quasi-period.

59. Suppose an undamped spring-mass system has a natural frequency of 2 seconds. A damping mechanism is then attached to the system so that the damping constant can be set to any desired value. What are all the possible quasi-periods the system could have?

---

The amplitude of an underdamped spring-mass system is $\displaystyle A\exp\left(-\frac{ct}{2m}\right),$ which decays exponentially. So if you know the mass and the damping constant, you can determine decay rate. And if you know the mass and measure the decay rate, you can determine the damping constant. Note that measuring the decay of the amplitude is usually much more difficult in practice than measuring the quasi-period. The quasi-period can be determined by measuring the times between the system passing through the equilibrium position, which means you can set the measuring devices in a fixed position. Since the amplitude changes, the measuring devices will need to observe at different positions to measure the amplitude.

The half-life of the amplitude (or anything else that decays exponentially) is the time it takes for the amplitude to decrease to half its starting value.

---

60. Suppose a spring-mass system has mass $500g$ and damping constant $750g/sec.$ What is the half-life of the amplitude of the system, i.e. how long does it take for the amplitude to be halved?

61. Suppose a spring-mass system has mass $100g$ and damping constant $80g/sec.$ What is the half-life of the amplitude of the system, i.e. how long does it take for the amplitude to be halved?

62. Suppose a spring-mass system has mass $2.0kg$ and the amplitude has a half-life of 0.4 seconds. What is the damping constant of the system?

63. Suppose a spring-mass system has mass $250g$ and the amplitude has a half-life of 4.5 seconds. What is the damping constant of the system?

 
64. A spring-mass system has mass $350g$ and spring constant $700g/sec^2.$ The damping constant can be adjusted to take any value. What is the smallest half-life that can be obtained without the system becoming overdamped?

65. A spring-mass system has mass $100g$ and spring constant $49g/sec^2.$ The damping constant can be adjusted to take any value. What is the smallest half-life that can be obtained without the system becoming overdamped?

66. The extreme points (max and min) of underdamped free motion $x(t)$ occur when $x'(t)=0.$ Show that the timing of the extreme points is periodic. Note that you don't have to actually solve $x'(t)=0.$ You just have to show the solutions are periodic.

67. Given that the extreme points occur at a set period from the previous problem, show that the ratio of the amplitudes of successive maxima is constant.

68. You attach a mass to an undamped spring, which causes it to stretch $1.4cm.$ You then pull the mass down and release it (with initial velocity 0), starting the spring in motion. How long will it take the mass to return to the position from which it was released (to the nearest $0.1 sec$)? Yes you do have enough information to solve this problem. Use $g=980cm/sec^2$ for the acceleration of gravity.

69. You attach a mass to an undamped spring, which causes it to stretch $3.2cm.$ You then pull the mass down and release it (with initial velocity 0), starting the spring in motion. How long will it take the mass to return to the position from which it was released (to the nearest $0.1 sec$)? Yes you do have enough information to solve this problem. Use $g=980cm/sec^2$ for the acceleration of gravity.

---

In designing systems to detect signals of various sorts, it is often useful to create a system that resonates at the frequency you wish to detect. This can happen with spring-mass systems used in seismographs or with LC circuits used in radio tuners. In the following problems you will need to remember that $\cos(at)$ has frequency $a/(2\pi)$ cycles per second.

---

70. Consider an undamped spring-mass system with mass of $340g.$ What spring constant will cause it to resonate at a frequency of 6 cycles per second.

71. Consider an undamped spring-mass system with mass of $50kg.$ What spring constant will cause it to resonate at a frequency of 0.2 cycles per second.

72. If you have a coil of 70 millihenrys, what capacitance do you need to have the circuit resonate at 60Hz (60 cycles per second)?

73. If you have a coil of 10 millihenrys, what capacitance do you need to have the circuit resonate at 1350kHz ($1.35\times10^6$ cycles per second)?

 
74. Show that for any unforced, overdamped system, there is
    1. a set of initial conditions such that the solution asymptotically approaches the equilibrium position (the origin), but never reaches it, and
    2. a set of initial conditions such that the solution passes through the equilibrium position (the origin) exactly once, and then approaches the equilibrium position asymptotically as $t\to\infty.$

75. Show that if any solution to a spring-mass system (or LRC circuit) passes through the equilibrium position more than once, it is underdamped.

---

As noted in the text, a forced undamped system can display the phenomenon of beats. The next few problems will go through the computations to explore this.

---

76. The general solution to the forced undamped system $mx''+kx=F_0\cos(\omega t)$ is $\displaystyle x(t)=\frac{F_0}{m(\omega_0^2-\omega^2)}cos(\omega t) + A\cos(\omega_0 t + \phi),$ where $\omega_0=\sqrt{k/m}$ and $A$ and $\phi$ are arbitrary constants. Show that with initial conditions $x(0)=0,$ $x'(0)=0,$ which correspond to starting the system from rest, the solution takes the form $x(t)=B(\cos(\omega t) - \cos(\omega_0 t))$ for some constant $B.$

77. Use the identity $\displaystyle \cos(a)-\cos(b)=2\sin\left(\frac{a+b}2\right) \sin\left(\frac{a-b}2\right),$ to rewrite the solution to the previous problem as a product of two sine waves.

78. You can think of a function of the form $B\sin(at)\sin(rt)$ with $r$ much larger than $a$ as a "fast" sine curve $\sin(rt)$ with slowly varying amplitude $B\sin(at).$ Each of these frequencies can be measured. Suppose the amplitude is varying with frequency $\displaystyle \frac{1}{4\pi}$ cycles per second. How close is the circular frequency of the forcing function, $\omega$ to the natural frequency $\omega_0$?

79. Find the general solution for $\displaystyle \frac{d^2y}{dx^2}+y=\sec(x).$

80. Given that $x^2$ and $x^3$ are homogeneous solutions for $\displaystyle x^2\frac{d^2y}{dx^2}-4x\frac{dy}{dx}+6y=\sqrt{x},$ find the general solution.

81. Given that $x$ and $x^{-1}$ are homogeneous solutions for $\displaystyle x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}-y=6x^2$, find the solution to the initial value problem with $y(1)=1$, $y'(1)=0$.

82. Solve the initial value problem $\displaystyle \frac{d^2y}{dx^2}+2\frac{dy}{dx}+5y=\ln(x)$, $y(1)=1$, $y'(1)=0$.

Answers to the odd numbered exercises.