Population Models
Discussion
My favorite application of first order differential equations is population dynamics. Several different models of population growth can be easily derived from what we know so far.Exponential Growth
Consider a bacterium. It reproduces by fission, that is every so often it splits into two new bacteria. The two progeny then undergo split into four bacteria sometime later. This process continues indefinitely. We represent this situation by saying that if there are $p$ bacteria now, we will add about $rp$ new bacteria every hour where $r$ is a constant of proportionality called the growth rate. Or in the standard calculus phrasing, the rate of change of $p$ is about $rp$ per hour, and if we start with $p_0$ bacteria we get the initial value problem $$ \frac{dp}{dt}=rp,\qquad p(0)=p_0 $$ where $p$ is the population of bacteria and $t$ is time in hours with the present time being set to $t=0$. This is a separable first order differential equation and we can solve it to find $$ p=p_0e^{rt}. $$ Hence the name exponential growth. The graph of population vs. time for this model is given below.
Logistic Growth
You may have noticed that in the preceeding model, the population explodes to $\infty$. Given a single bacterium, you should grow a colony the size of the earth in a matter of days. Of course this doesn't happen. The previous model provides a model of the ``birth'' of new individuals but makes no allowance for the death of individuals. Bacteria do not usually die of old age, but they do die from competition for resources. We add this to the model by saying the rate of deaths in the population is proportional to the likelihood of contacts between two individuals (which is usually assumed to be proportional to $p^2$). This leads to the model $$ \frac{dp}{dt}=rp-kp^2=rp(1-(k/r)p),\qquad p(0)=p_0 $$ where $k$ is a constant of proportionality. This is also a separable equation (as all the equations in this section will be) but it is easiest to analyze it using the ideas of the previous section rather than trying to solve the equation directly. The equilibrium points of the equation are at $p=0$, and $p=r/k$. The equilibrium point at $p=0$ is unstable while the equilibrium point at $p=r/k$ is stable. $r/k$ is called the carrying capacity of the model. So the population should increase to a level $p=r/k$ and then stay there. This is much more in line with what we expect to happen to a population of bacteria. The graph of population vs. time for this model is given below.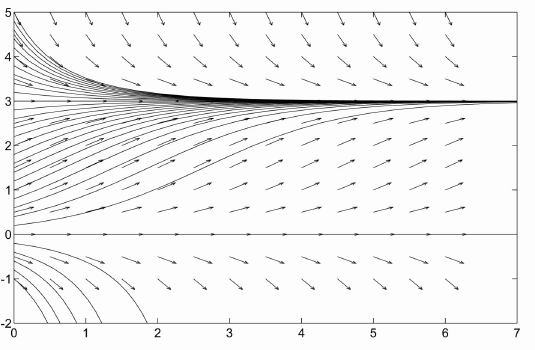
Exponential Decay
Large creatures (rabbits, whales, us, etc.) do not reproduce by fission. If you take a rabbit, it doesn't split into two as time passes. It sits there quietly for a few years and then it dies. Mathematically, you could write that some proportion of rabbits dies every year so the negative rate of change of the population of rabbits is proportional to the population. Assuming an initial population $p_0$ this gives rise to the model $$ \frac{dp}{dt}=-cp,\qquad p(0)=p_0 $$ where $p$ is the population of rabbits, $t$ is time (in years) and $c$ is a constant of proportionality. We can solve this initial value problem to find the poplulation is $$ p(t)=p_0e^{-ct} $$ This is clearly not a reasonable model for rabbits. But it is a reasonable model for the population of Carbon-14 molecules in fossil materials. One of the nice features of population dynamics is that it can be applied to many different sorts of populations, from rabbits to U-235 nuclei. The graph of population vs. time for this model is given below.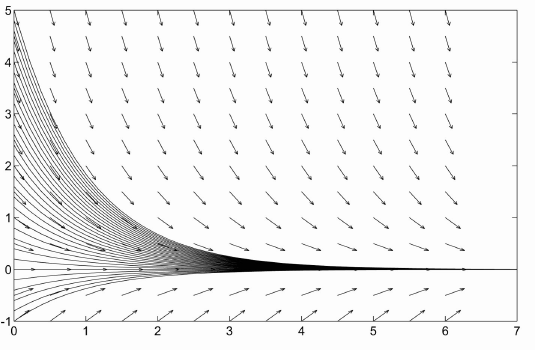
Exponential Growth With Threshold
Returning to rabbits, the population of rabbits doesn't just fade away to nothing in real life. Our problem earlier with bacteria was failing to include death in our model. Our current problem is failing to include birth. We may assume that a certain percentage of interactions between two rabbits will lead to the birth of several new baby rabbits. The revised model is then $$ \frac{dp}{dt}=-cp+rp^2=-cp(1-(r/c)p),\qquad p(0)=p_0 $$ The equilibrium points for this equation are $p=0$ and $p=c/r$. $c/r$ is called the threshold. $p=0$ is stable while $p=c/r$ is unstable. So if the population falls below the threshold, $c/r$, needed to sustain itself, it will die off. If the population starts above the threshold, it will explode to $\infty$. The graph of population vs. time for this model is given below.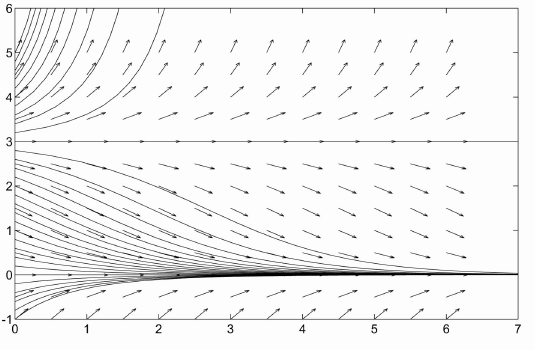
Logistic Growth With Threshold
Of course the population of rabbits doesn't tend to $\infty$ (though you couldn't prove it by my garden). Rabbits also experience competition for scarce resources. Since interactions of 2 rabbits are presumed to have positive effects, we subtract a term proportional to the interactions of 3 rabbits ($p^3$) to model competitive pressures. This gives the model $$ \frac{dp}{dt}=-cp+rp^2-kp^3,\qquad p(0)=p_0. $$ Now we have three equilibrium points (assuming $r^2>4kc$), $0$, $p_u=(r-\sqrt{r^2-4kc})/(2k)$ and $p_s=(r+\sqrt{r^2-4kc})/(2k)$. 0 is a stable equilibrium point. $p_u$ is an unstable equilibrium point and is called the threshold as in the previous example. $p_s$ is a stable equilibrium point, called the carrying capacity as in logistic growth. So if the populations falls below the threshold $p_u$ it dies out but otherwise it tends to the level $p_s$. Looking at the graphs of the population vs. time, you should note that the behavior above the threshold closely resembles the behavior of the logistic growth model. For established populations, the logistic growth model we established for bacteria is often used because it is simpler and has the right general properties (and population dynamics is by no means as accurate a subject as physics). Logistic growth with threshold is used in studying populations in danger of extinction, such as blue whales. The graph of population vs. time for this model is given below.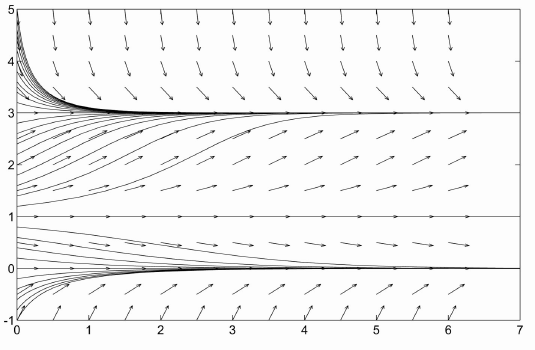
If you have any problems with this page, please contact bennett@ksu.edu.
©1994-2025 Andrew G. Bennett