Geometric Interpretation - Numerical Methods
Initial Discussion
So far we have learned some algebraic techniques for solving first order differential equations of various special forms. We will learn more techniques in the future, but we will still be restricted to solving just selected equations of special form. Most first order equations can't be solved explicitly, even in integral form. That being the case, it is often most useful to have a numerical technique to approximate the solution. We will consider the two simplest numerical methods for approximating solutions, Euler's method and the improved Euler's method. These techniques build on the geometric interpretation of differential equations that we developed in the last lab. We will consider the example $$ \frac{dy}{dx}=2x-y,\qquad y(0)=1. $$
Geometrically, this solution is the curve that follows the arrows of the
slope field and passes through the point (0,1). We can build an
approximation to this curve as follows. Suppose we want to
approximate the value of $y$ at $x=0.1.$ Start at the point (0,1). At this
point the slope is $2\times0-1=-1.$ So our arrow points down with slope
$-1.$
We follow this arrow as pictured at the left to get
$y(0.1)\approx 1-1\times0.1 = 0.9.$
Since the exact value of $y(0.1)=0.91452\ldots$, this is a reasonably good
approximation.
You might observe that this is exactly the same thing as using the tangent
line approximation from Calculus. And just like the tangent line
approximation, it works reasonably well as long as your target $x$ (in
this case 0.1) is close enough to your starting $x$ (in this case 0). It
breaks down if you try to get too far away from your initial value. For
example, if you try to approximate $y(1)$ using this technique, you get
$y(1)\approx1-1\times1=0$, but the exact value is $y(1)=1.103638\ldots$. As
you can see from the picture above, the slope field changes at each point
causing the yellow solution curve to bend up instead of just continuing in
the same downward direction of the initial arrow. To deal with the
problem of changing slopes, we need to make many small steps following
each arrow for a short distance and then computing the new slope (the
new arrow), repeating the process until we reach our target value.
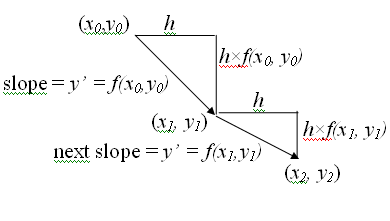We call
the horizontal length of each short step the step size in this
process. It will be helpful to introduce some notation as we start
repeating our approximation process for multiple steps. For the
initial value problem
$$
\begin{align}
\frac{dy}{dx}&=f(x,y) \\
y(x_0)=y_0
\end{align}
$$
so the
starting point is $(x_0,y_0)$, we call our step size $h$ and then define
\begin{align}
x_{n+1}&=x_n+h \\
y_{n+1}&=y_n+hf(x_n,y_n)
\end{align}
For example, to approximate $y(0.3)$ using a step size of 0.1 we compute
$$\begin{align}
x_0=0\qquad\qquad y(0)&=y_0=1 \\
x_1=0+0.1=0.1\qquad y(0.1)&\approx y_1=1+0.1(2\times0-1) = 0.9 \\
x_2=0.1+0.1=0.2\qquad y(0.2)&\approx y_2=0.9+0.1(2\times0.1-0.9) = 0.83 \\
x_3=0.2+0.1=0.3\qquad y(0.3)&\approx y_3=0.83+0.1(2\times0.2-0.83) = 0.787
\end{align}
$$
Implementing Euler's Method in Excel
This sort of repetitive calculation is exactly what computers were invented to do. While you can carry out the assignment below by hand, you will probably want to program this algorithm into a computer. A spreadsheet is well suited to this process, though if you want to cook up a program in your favorite language to carry out the computations instead, be my guest. Open Excel (or your favorite spreadsheet if you are working on your own computer). We'll start by labeling the columns to keep track of what goes where. Enterx into cell A1, y' into cell
B1, y into cell C1, and h into cell H1. Next put
the initial values and step-size into the appropriate starting spots with
0 in cell A2, 1 in cell C2, and 0.1
in cell H2. Then put in the formulas with =A2+$H$2 in cell
A3, =2*A2-C2 in cell B3, and =C2+$H$2*B3 in
cell
C3 (we'll discuss the meaning of the $ signs in these
formulas below).
You now have the x
column set to add the step size
h as you move down each row, the y' column to
compute the slope based on the starting x and y
values, and the y column to add h times
y' to the previous y. Now click and drag to select cells
A3..C3 and then click on the small square at the lower right of the box
around those cells and drag it down for a dozen rows or so. This will copy
the formulas down and automates the repetitive calculation of each step.
Note that if you click now on cell A4 it shows the formula
=A3+$H$2. Comparing this to the original formula you
copied from cell A3, =A2+$H$2, you see the spreadsheet
recognizes that as you pull down the formula, you want to update the
reference from cell A2 to cell A3 as you pull
down. However, the reference to cell H2 hasn't changed (which
is good because you still wanted to reference the same step-size). This is
what the $ signs did - they told the spreadsheet the
reference was
absolute, not relative, and shouldn't update when you pulled the formula
down.
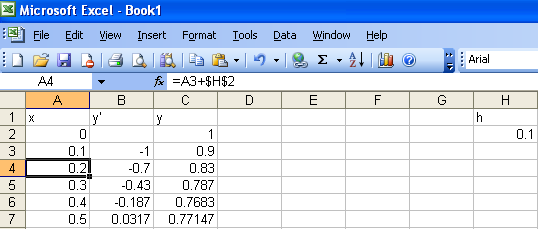
y' in column B. Do
be sure to copy the edited formula down the whole column.
Since our example equation $\displaystyle\frac{dy}{dx}=2x-y$ is
linear, we can
find the exact answer to our initial value problem is $y=3\exp(-x)+2x-2$.
This allows us to check how close Euler's method comes to approximating
the true solution. In cell D1 of the spreadsheet enter y
exact and in cell E1 enter rel error (which stands for
relative error). Then in cell D2 enter =3*exp(-A2)+2*A2-2 and
in cell E2 enter =(D2-C2)/D2. It will be convenient to
right-click on cell E2 and Format Cells as Percentage since relative error
is a percent. Now click and drag to select cells D2 and E2 and drag those
formulas down. This will show you how accurate the approximation produced
by Euler's method is.
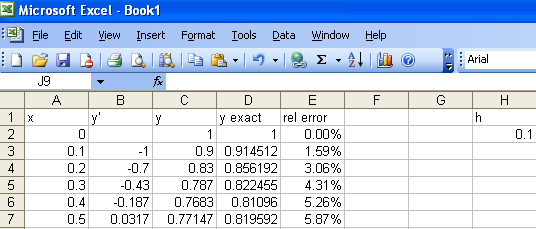
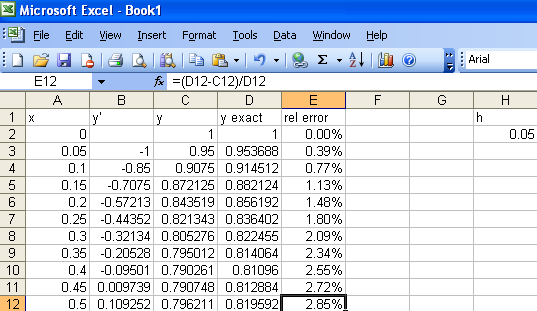
0.05 to cut the step size in half, you find that the error in
the value of $y(0.5)$ has been cut from 5.87% to 2.85%. Of course you had
to take 10 steps of size 0.05 to get to 0.5 while it only took 5 steps of
size 0.1. So you do twice as much work but you cut the error roughly in
half. This is actually the standard pattern.
The Improved Euler Method (Heun's Method)
Just shrinking the step size isn't always practical as a way to improve accuracy in Euler's method. Since you use the results from each step in the next round of calculations, roundoff error will build up as you proceed. If you make the step size too small, you can build up so much roundoff error that it swamps the "discretization error" built into the approximation. You also slow down your calculations with small step sizes since it takes so many steps to get where you are going. Some extra work getting a more accurate approximation than the tangent line approximation will pay off. This leads to the Improved Euler Method, which is also sometimes called Heun's Method.
So how can we improve our approximation for
$\displaystyle\frac{dy}{dx}=f(x,y)$, $y(x_0)=y_0$? Well what we are
looking for is
not the tangent line to the curve, we are looking for the "secant" line
between the points $(x_0,y(x_0))$ and $(x_1,y(x_1))$. Then the formula for
the secant line is $y(x_1)=y(x_0)+(x_1-x_0)S$ where $S$ is the slope of
the secant line. So how can we approximate the slope of the secant line?
Euler's method uses the slope of the tangent line at the
left endpoint $y'=f(x_0,y(x_0))$ as the approximation to the slope of the
secant
line. Geometrically, there is no reason why the left endpoint should give
a better approximation than the slope at the right endpoint,
$y'=f(x_1,y(x_1))$.
In fact, the average of
the slopes of the tangent lines at each endpoints
$$
\frac{f(x_0,y(x_0))+f(x_1,y(x_1))}2
$$
is better still.
Unfortunately, we only know the left endpoint $(x_0,y_0)$; the right
endpoint $(x_1,y(x_1))$ is what we are trying to find (which is why we used
the left endpoint in Euler's method). But once we have
carried out Euler's method, we have an approximation to the right
endpoint, $(x_1,y_1)$. Now we can use this approximation to compute the
approximate slope of the tangent line at the right endpoint
$y'=f(x_1,y_1)$
and then the
approximate slope of the secant line
$$
\frac{f(x_0,y_0)+f(x_1,y_1)}2
$$
All those "approximates" in the
last sentence may look scary, but the process is actually fairly
straightforward. For the initial value problem
$$ \frac{dy}{dx}=2x-y,\qquad y(0)=1,$$
we set $x_0=0$ and $y_0=1$ and compute $x_{n+1}=x_n+h$ and
$$
\begin{align}
x_{n+1}&=x_n+h \\
\tilde y_{n+1}&=y_n+h(2x_n-y_n)
\end{align}
$$
as in Euler's method. We then improve our approximation for $y(x_{n+1})$
from $\tilde y_{n+1}$ to
$$
y_{n+1}=y_n+h\left(\frac{(2x_n-y_n)+(2x_{n+1}-\tilde y_{n+1})}{2}\right)
$$
We repeat this procedure as many times as needed to reach our desired
point just as with the original Euler's method. For example, to
approximate $y(0.3)$ using a step size of 0.1 we compute the following
(calculations here have only been reported to 4 decimal places):
$$
\begin{align}
x_1&=0+0.1=0.1 \\
\tilde y_1&=1+.1(2\times0-1)=.9 \\
y_1&=1+.1\left(\frac{(2\times0-1)+(2\times.1-.9)}{2}\right)
=.915 \\
& \\
& \\
x_2&=0.1+0.1=0.2 \\
\tilde y_2&=.915+.1(2\times.1-.915)=.8435 \\
y_2&=.915+.1\left(\frac{(2\times.1-.915)+(2\times.2-.8435)}{2}\right)
=.8571 \\
& \\
& \\
x_3&=0.2+0.1=0.3 \\
\tilde y_3&=.8571+.1(2\times.2-.8571)=.8114 \\
y_3&=.8571+.1\left(\frac{(2\times.2-.8571)+(2\times.3-.8114)}{2}\right)
=.8237
\end{align}
$$
Implementing The Improved Euler Method In Excel
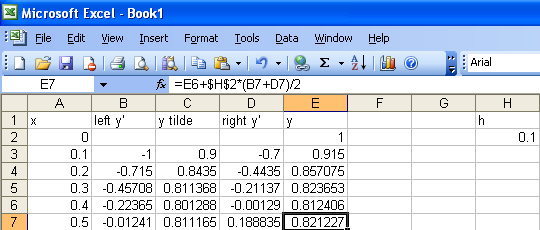
Just as for Euler's method, the repeated calculations of the improved Euler method are best handled with a computer. As before, you can use whatever tool you find most appropriate, but the simplest is probably the spreadsheet. Open up your favorite spreadsheet. We set things up similarly to the Euler's method, but with a couple of extra columns now for the extra computations. Enterx in cell A1, left y' in
cell B1, y tilde in cell C1, right y' in cell
D1, y in cell E1, and h in cell H1. Next enter
the initial values 0 in cell A2, 1 in cell E2,
and 0.1 in cell H2. Then enter the formulas
=A2+$H$2 in cell A3, =2*A2-E2 in cell B3,
=E2+$H$2*B3 in cell C3, =2*A3-C3 in cell D3, and
=E2+$H$2*(B3+D3)/2 in cell E3. Now click and drag to select
A3..E3 and then copy the formula down the sheet to repeat the calculations
as far as you want.
y exactrel error=3*exp(-A2)+2*A2-2=(F2-E2)/F2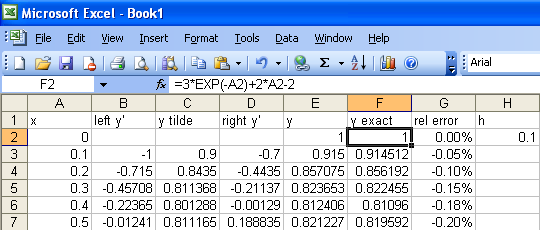
Concluding Discussion
We could repeat the process of improving the estimate by using both $\tilde y_1$ and $y_1$ from the improved Euler's method to get a New And Improved Euler's method. And of course we could then improve the estimate another time and yet another time. This leads to a class of methods called Runge-Kutta methods. To find the best approximations of the slope by taking weighted averages of different simpler approximations at different points requires that we replace the simple tangent line approximation by a Taylor series approximation and do some more algebra. But since that's all been done, you can just look up the formulas and enter them into a spreadsheet in the same manner as we've done here. Of course, applying these methods requires you to pick the correct step size. Looking back at the geometry you should realize there is no reason you have to always use the same step size. Indeed, you will be better off if you vary the step size to be small where the solution is curving quickly and a larger step size (hence fewer steps so quicker execution and less roundoff) where the solution is moving in more of a straight line. In developing code to track the motion of space probes (which have long straight paths between planets and complicated curves as the swing around planets), Fehlberg developed a further refinement using two different Runge-Kutta methods where you compare their answers to get an approximation for the error. This approximation can then be used to adjust the step size automatically. These are called Runge-Kutta-Fehlberg methods and are perhaps the best of the common techniques for finding careful approximations to initial value problems. While the RKF techniques are recommended for careful approximations, the methods we've learned here, besides introducing the basic ideas, are also useful when you need rough approximations quickly. Being so simple, Euler's method and the improved Euler's method will run quicker than more accurate techniques. The physics model of many video games is implemented using these methods. To update the screen 60 times a second, you need to compute the position of many different objects as quickly as possible. And you just need things to look and feel right to the players; you don't need precise answers (for example, any error less than one pixel is irrelevant). In this situation, using Euler's method or the improved Euler's method is the best choice.Exercises
Approximate $y(2)$ for each of the initial value problems using Euler's method, first with a step size of $h=.1$ and then with a step size of $h=.05$.- $\displaystyle\frac{dy}{dx}=2xy,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=3y,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x-y}{x+2y},\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x^2-2xy}{x^2+2y^2},\qquad y(0)=-1$
- $\displaystyle\frac{dy}{dx}=y+x,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=x-y,\qquad y(0)=2$
- $\displaystyle\frac{dy}{dx}=2xy,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=3y,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x-y}{x+2y},\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x^2-2xy}{x^2+2y^2},\qquad y(0)=-1$
- $\displaystyle\frac{dy}{dx}=y+x,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=x-y,\qquad y(0)=2$
- $\displaystyle\frac{dy}{dx}=2xy,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=3y,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x-y}{x+2y},\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=\frac{x^2-2xy}{x^2+2y^2},\qquad y(0)=-1$
- $\displaystyle\frac{dy}{dx}=y+x,\qquad y(0)=1$
- $\displaystyle\frac{dy}{dx}=x-y,\qquad y(0)=2$
If you have any problems with this page, please contact bennett@math.ksu.edu.
©2010, 2014 Andrew G. Bennett