THEOREM:
If a continuous function $G(x)$ has the property that $$\int_{a}^{c} G(x)h(x)dx =0$$ for all smooth functions $h(x)$ with $h(a)=0=h(c)$, then $G(x)\equiv 0$ for all $x$ in the interval $(a,c)$.SKETCH OF PROOF:
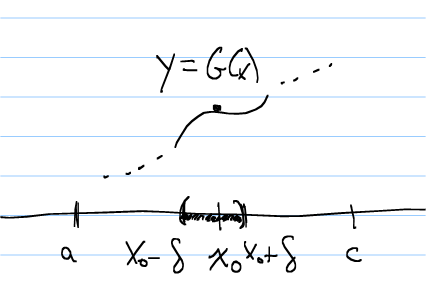The idea here is that if there is a point $x_0$ where $G(x_0)\ne 0$, then
there we can find a smooth function $h(x)$ such that
$\int_{a}^{c} G(x)h(x)dx \ne 0$. Since we are given the integral is 0 for
all choices of $h(x)$, it follows that we must have $G(x) = 0$ at all
points.
So to start we assume we have a point $x_0$ with $G(x_0)\ne 0$. We suppose
that $G(x_0)>0$ (the proof for the case where $G(x)<0$ is almost
identical, just change the words positive and negative where needed). Now
since $G(x)$ is continuous, there must be some little interval of
$x_0$ where $G(x)>0$ for all points in the interval, say $(x_0-\delta,
x_0+\delta)$ as pictured. Note that $G(x)$ might be positive for a ways
outside the interval, or it might be negative or 0. We only need to know
that $G(x)>0$ for every point in the interval.
Now we pick a "bump function" $h(x)$ which is identically 0 outside the
interval
$(x_0-\delta,x_0+\delta)$, but is positive for all the points in the
interval, as pictured. Then we compute the integral of $G(x)h(x)$. Since
$h(x)=0$ for all points outside the interval, $G(x)h(x)=0$ for all points
outside the interval, so
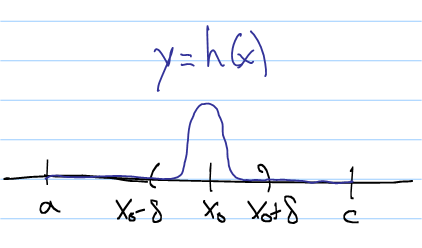$$\int_{a}^{c} G(x)h(x)dx =
\int_{x_0-\delta}^{x_0+\delta} G(x)h(x)dx $$
(this is why we didn't care what $G(x)$ did outside the interval). On the
other hand, we know both $G(x)>0$ and $h(x)>0$ for all points in the
interval, so $G(x)h(x)>0$ for all points in the interval
$(x_0-\delta,x_0+\delta)$. And if the function is everywhere positive,
there is no chance of cancellation so the integral must also be positive,
i.e.
$$\int_{x_0-\delta}^{x_0+\delta} G(x)h(x)dx > 0.$$
But this contradicts the given condition that the integral is always 0.
So the only way to have the integral be 0 for all choices of $h(x)$ is to
have $G(x)=0$ for all values of $x$ between $a$ and $c$.
Return to Calculus of Variations
If you have any problems with this page, please contact bennett@math.ksu.edu.
©2010, 2014 Andrew G. Bennett