Long Term Behavior of Solutions
Discussion
Now we will examine the qualitative behavior of solutions to first order initial value problems of the form $$ \frac{dP}{dt}=f(P),\qquad\qquad P(0)=P_0 $$ with particular emphasis on their long term behavior. A first order equation of the above form, where the right hand side depends only on the dependent variable, $P$, and not on the independent variable, $t$, is called autonomous. Our goal is to be able to draw the solution curves just from looking at the function $f(P)$ in the equation $$ \frac{dP}{dt}=f(P).$$ Then in the next couple of sections we will develop and analyze models of population growth using the techniques we develop here. We start by looking for equilibrium points for the differential equation. An equilibrium point for the differential equation $dP/dt=f(P)$ is a value $P_0$ which satisfies $f(P_0)=0$. Suppose $P_0$ is an equilibrium point for our differential equation. Then $P=P_0$ is a solution to the differential equation. We quickly check that $dP/dt=0=f(P)$ since $P_0$ is a constant and $f(P_0) = 0$. So if our initial value is $P(0)=P_0$, our solution is just a straight line (and $P$ is unchanging, hence in equilibrium). Now since the solution curves don't cross each other (as long as $f(P)$ is continuous), we know that if $P(0)<P_0$, then $P(t)<P_0$ for all $t$. Similarly if $P(0)>P_0$, then $P(t)>P_0$ for all $t$. Next by examining the sign of $dP/dt$ at $P(0)$ we can determine whether $P(t)$ is increasing or decreasing. For autonomous equations $P(t)$ will continue to increase or decrease until it encounters an equilibrium point, which will be a barrier since $P(t)$ can't cross an equilibrium point. If no equilibrium point is encountered, then $P(t)$ will increase or decrease without bound. This information is enough to let us determine the long term behavior of $P(t)$.Paradigm
What is the long term behavior of the solution to $$\frac{dP}{dt}=\frac14(P^2+P-2)$$ Step 1: Find the equilibrium points. We solve $\frac14(P^2+P-2)=0$ and find the equilibrium points are $P_0=-2$ and $P_0=1$. Step 2:Find the sign of $dP/dt$ in the regions between equilibrium points and classify $P$ as increasing or decreasing in these regions. If $P<-2$ then $\frac14(P^2+P-2)>0$ so $dP/dt>0$ and so $P$ is increasing. If $-2<P<1$ then $\frac14(P^2+P-2)<0$ so $dP/dt<0$ and so $P$ is decreasing. If $P>1$ then $\frac14(P^2+P-2)>0$ so $dP/dt>0$ and $P$ is increasing. Step 3: The limiting value is calculated by using the rule that $P$ will increase or decrease in a given region until it encounters a "barrier" formed by an equilibrium point. If no such barrier is encountered, $P$ increase or decreases without bound (to $\pm\infty$). If $P<-2$ then $P$ will increase until it hits the barrier formed by the solution curve corresponding to the equilibrium point at $P=-2$, so in the limit as $t\to\infty$, $P\to-2$. If $-2<P<1$ then $P$ is decreasing, but $P$ can only decrease until it hits the barrier formed by the solution curve corresponding to the equilibrium point at $P=-2$, so in the limit as $t\to\infty$, $P\to-2$. If $P>1$ then $P$ is increasing and there is no barrier so $P\to\infty$. The graph of the vector field and solution curves is shown below.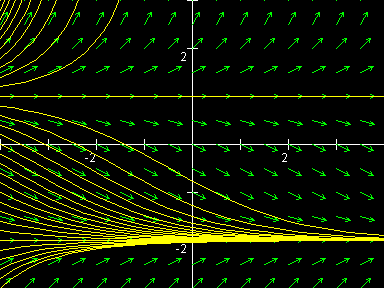
More Discussion
Note that I didn't say that for $P>1$, $P\to\infty$ as $t\to\infty$. The reason I didn't say this is that it isn't true. It doesn't take infinitely long for $P$ to get to $\infty$, it explodes to $\infty$ in finite time. When you have a differential equation of the form $dP/dt=f(P)$ where $f(P)$ is a polynomial, and you have a solution to the differential equation which tends to $\pm\infty$, then the solution explodes to $\pm\infty$ in finite time if the polynomial $f(P)$ is of degree 2 or greater. If $f(P)$ is a first degree polynomial then the solution politely tends to $\pm\infty$ in infinite time. This is one reason for doing a geometric rather than an analytic analysis of the long term behavior of solutions. It is clear from the geometric analysis what is happening. But if you solve the equation analytically and then take the limit as $t\to\infty$, you will get the wrong answer because you will cross the singularity at the explosion. There are examples like this in the exercises. Note that if $P=-2$ but then gets "bumped" a little bit away, $P$ will return to -2. We say $P=-2$ is a stable equilibrium point. On the other hand, if $P=1$ gets "bumped" a little bit, $P$ will tend to move away from 1, toward either $\infty$ or $-2$. We say $P=1$ is an unstable equilibrium point. The practical rule is that $P$ will tend to a stable equilibrium point, or $\pm\infty$, since in practice whatever situation you are looking at will eventually get "bumped." This rule is only true for autonomous equations; the situation is much more complicated for general equations where the right hand side depends on $t$ as well as $P$. But this rule will suffice for now.If you have any problems with this page, please contact bennett@ksu.edu.
©1994-2025 Andrew G. Bennett